
分析 (1)根据多项式乘多项式展开,然后再合并同类项即可解答本题;
(2)根据同底数幂的乘法、幂的乘方和积的乘方进行计算即可;
(3)根据单项式乘多项式进行计算即可;
(4)根据单项式乘多项式先将原式展开然后再合并同类项即可解答本题;
(5)根据单项式乘多项式,先去小括号,再去中括号即可解答本题;
(6)根据积的乘方、同底数幂的乘法对原式展开再合并同类项即可解答本题.
解答 解:(1)(3x+1)(x-2)
=3x2-6x+x-2
=3x2-5x-2;
(2)a4•a4+(a2)4-(3a4)2
=a8+a8-9a8
=-7a8;
(3)-2x2y(3x2-2x-3)
=-6x4y+4x3y+6x2y;
(4)a(a+b)-b(a+b)
=a2+ab-ab-b2
=a2-b2;
(5)4ab[2a2-3b(ab-ab2)]
=4ab[2a2-3ab2+3ab3]
=8a3b-12a2b3+12a2b4;
(6)(-3a)3-(-a)•(-3a)2
=-27a3+a×9a2
=-27a3+9a3
=-18a3.
点评 本题考查整式的混合运算,解题的关键是明确整式的混合运算的计算方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
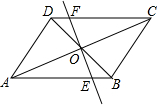 如图,在?ABCD中,对角线AC与BD相交于点O,∠ADB=90°,过O作EF⊥AC交AB于E,交CD于F.
如图,在?ABCD中,对角线AC与BD相交于点O,∠ADB=90°,过O作EF⊥AC交AB于E,交CD于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
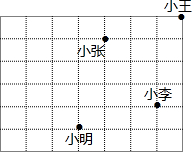 建立适当的直角坐标系,使得小明坐标为(3,-1),写出小张、小王、小李的坐标:
建立适当的直角坐标系,使得小明坐标为(3,-1),写出小张、小王、小李的坐标:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com