
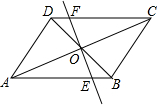
 如图,在?ABCD中,对角线AC与BD相交于点O,∠ADB=90°,过O作EF⊥AC交AB于E,交CD于F.
如图,在?ABCD中,对角线AC与BD相交于点O,∠ADB=90°,过O作EF⊥AC交AB于E,交CD于F.分析 (1)连接AF、EC,由△FCO≌△EAO得FC=AE,得到四边形FCEA是平行四边形,只要证明FA=FC即可.
(2)作DM⊥AC于M,用面积法求出DM,根据sin∠DCM=sin∠EAO即可解决问题.
解答 (1)证明:如图连接AF、EC,
∵四边形ABCD是平行四边形,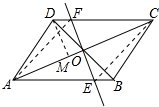
∴CD∥AB,AO=OC,
∴∠FCO=∠EAO,
在△FCO和△EAO中,
$\left\{\begin{array}{l}{∠FCO=∠EAO}\\{CO=AO}\\{∠FOC=∠EOA}\end{array}\right.$,
∴△FCO≌△EAO,
∴FC=AE,
∵FC∥AE,
∴四边形FCEA是平行四边形,
∵FO⊥AC,OA=OC,
∴FA=FC,
∴四边形FCEA是菱形.
(2)作DM⊥AC于M,
在RT△ADB中,∵AD=4,AB=2$\sqrt{13}$,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=6,
∵四边形ABCD是平行四边形,
∴DO=OB=3,AO=$\sqrt{A{D}^{2}+D{O}^{2}}$=5,DC=AB=2$\sqrt{13}$,
∵$\frac{1}{2}$•AD•DO=$\frac{1}{2}$•OA•DM,
∴DM=$\frac{12}{5}$,
∴sin∠DCA=$\frac{DM}{DC}$=$\frac{6\sqrt{13}}{65}$,
∵∠DCA=∠CAE,
∴sin∠CAE=$\frac{OE}{AE}=\frac{6\sqrt{13}}{65}$,
由(1)可知△FCO≌△EAO
∴OF=OE,EF=2OE,
∴$\frac{EF}{AE}$=$\frac{12\sqrt{13}}{65}$,
∴$\frac{AE}{EF}$=$\frac{5\sqrt{13}}{12}$.
点评 考查了菱形的判定和性质、平行四边形的判定和性质、勾股定理、三角函数等知识,第二个问题的关键是作高DM,转化为在RT△DCM求出sin∠DCM,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
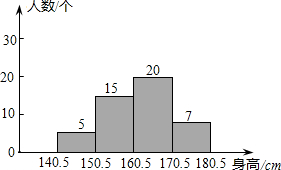 某校测量了初三(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如图频数分布直方图,则下列说法正确的是( )
某校测量了初三(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如图频数分布直方图,则下列说法正确的是( )| A. | 该班人数最多的身高段的学生数为7人 | |
| B. | 该班身高最高段的学生数为7人 | |
| C. | 该班身高最高段的学生数为20人 | |
| D. | 该班身高低于160.5cm的学生数为15人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,AB=4,BC=8,∠B=60°,点P以每秒2个单位速度,从点B出发沿射线BA方向运动,同时直线l以每秒1个单位速度,从CD出发沿射线CB方向运动,分别交BC,AC于点G,H,连结PG,设运动的时间为t,当G与B重合时,运动停止.
如图,在?ABCD中,AB=4,BC=8,∠B=60°,点P以每秒2个单位速度,从点B出发沿射线BA方向运动,同时直线l以每秒1个单位速度,从CD出发沿射线CB方向运动,分别交BC,AC于点G,H,连结PG,设运动的时间为t,当G与B重合时,运动停止.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>n | B. | m<n | C. | k>0 | D. | k<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com