
 如图所示,已知:AB是⊙O的直径,CB是⊙O的弦,过点B作BD⊥CP于D,若CP是⊙O的切线.
如图所示,已知:AB是⊙O的直径,CB是⊙O的弦,过点B作BD⊥CP于D,若CP是⊙O的切线.| 1 |
| 6 |
| ||
| 4 |
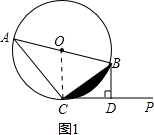 解:(1)如图1,连接OC,
解:(1)如图1,连接OC,
| ||
| 4 |
| 60ππr2 |
| 360 |
| 1 |
| 6 |
| 1 |
| 6 |
| ||
| 4 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

| A、3π | ||
| B、4π | ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、三点确定一个圆 |
| B、对角线互相垂直且相等的四边形是正方形 |
| C、若Rt△ABC中,∠C=90°,则sinA=cosB |
| D、三角形的内心到三角形三个顶点的距离相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 在一自助夏令营活动中,小明同学从营地A出发,要到A地的北偏东45°方向的C处,他先沿正东方向走了100m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如上图),那么,由此可知,B、C两地相距为
在一自助夏令营活动中,小明同学从营地A出发,要到A地的北偏东45°方向的C处,他先沿正东方向走了100m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如上图),那么,由此可知,B、C两地相距为查看答案和解析>>
科目:初中数学 来源: 题型:
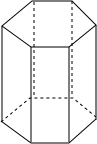 如图,是一个正六棱柱,它的底面边长是3cm,高是6cm.
如图,是一个正六棱柱,它的底面边长是3cm,高是6cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com