
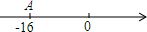 已知AB两地相距50单位长度,小明从A地出发去B地,以每分钟2个单位长度的速度行进,第一次他向左1单位长度,第二次他向右2单位长度,第三次再向左3单位长度,第四次又向右4单位长度…,按此规律行进,如果A地在数轴上表示的数为-16.
已知AB两地相距50单位长度,小明从A地出发去B地,以每分钟2个单位长度的速度行进,第一次他向左1单位长度,第二次他向右2单位长度,第三次再向左3单位长度,第四次又向右4单位长度…,按此规律行进,如果A地在数轴上表示的数为-16.分析 (1)由题意可得点B位于点A的左侧或右侧,AB两地相距50单位长度,A地在数轴上表示的数为-16,可以得到B地在数轴上表示的数;
(2)根据题意可以发现奇数次运动和偶数次运动是有一定规律的,从而可以得到第八次行进后小明到达点P,此时点P与点B相距几个单位长度和八次运动完成后一共经过了几分;
(3)根据题意可以发现奇数次运动和偶数次运动是有一定规律的,从而可以写出n为偶数和奇数时,在数轴上点Q表示的数是什么.
解答 解:(1)∵AB两地相距50单位长度,A地在数轴上表示的数为-16,
∴点B表示的数为:-16-50=-66或-16+50=34,
即B地在数轴上表示的数是-66或34;
(2)由题意可得,
第一次运动到点:-16-1,
第二次为:-16-1+2=-16+1,
第三次为:-16+1-3=-16-2,
第四次为:-16-2+4=-16+2,
由上可得,第奇数次运动到点-16-$\frac{n+1}{2}$,第偶数次运动到点:-16+$\frac{n}{2}$,
∴第八次运动到点P为:-16+$\frac{8}{2}=-16+4=-12$,
∵B地在原点的右侧,
∴点B表示的数为:34,
∴点P与点B相距的单位长度为:34-(-12)=46,
∴八次运动完成后经过的时间为:(1+2+3+4+5+6+7+8)÷2=36÷2=18(分钟),
即B地在原点的右侧,经过第八次行进后小明到达点P,此时点P与点B相距46个单位长度,八次运动完成后一共经过了18分钟;
(3)由题意可得,
第一次运动到点:-16-1,
第二次为:-16-1+2=-16+1,
第三次为:-16+1-3=-16-2,
第四次为:-16-2+4=-16+2,
由上可得,第奇数次运动到点-16-$\frac{n+1}{2}$,第偶数次运动到点:-16+$\frac{n}{2}$,
即当n为奇数时,在数轴上点Q表示的数为:-16$-\frac{n+1}{2}$;当n为偶数时,在数轴上点Q表示的数为:-16$+\frac{n}{2}$.
点评 本题考查一元一次方程的应用和数轴,解题的关键是明确题意,发现题目中的规律,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
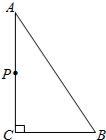 如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).
如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第三、四象限 | D. | 第一、二象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com