
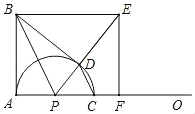
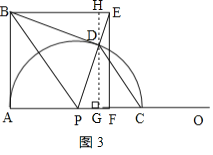
【题目】如图,∠BAO=90°,AB=8,动点P在射线AO上,以PA为半径的半圆P交射线AO于另一点C,CD∥BP交半圆P于另一点D,BE∥AO交射线PD于点E,EF⊥AO于点F,连接BD,设AP=m.
(1)求证:∠BDP=90°.
(2)若m=4,求BE的长.
(3)在点P的整个运动过程中.
①当AF=3CF时,求出所有符合条件的m的值.
②当tan∠DBE=![]() 时,直接写出△CDP与△BDP面积比.
时,直接写出△CDP与△BDP面积比.
【答案】(1)详见解析;(2)![]() 的长为10;(3)m的值为
的长为10;(3)m的值为![]() 或
或![]() ;
;![]() 与
与![]() 面积比为
面积比为![]() 或
或![]() .
.
【解析】
![]() 由
由![]() 知
知![]() ,再由
,再由![]() 知
知![]() 、
、![]() ,据此可得
,据此可得![]() ,证
,证![]() ≌
≌![]() 即可得;
即可得;![]() 易知四边形ABEF是矩形,设
易知四边形ABEF是矩形,设![]() ,可得
,可得![]() ,证
,证![]() ≌
≌![]() 得
得![]() ,在
,在![]() 中,由
中,由![]() ,列方程求解可得答案;
,列方程求解可得答案;![]() 分点C在AF的左侧和右侧两种情况求解:左侧时由
分点C在AF的左侧和右侧两种情况求解:左侧时由![]() 知
知![]() 、
、![]() 、
、![]() ,在
,在![]() 中,由
中,由![]() 可得关于m的方程,解之可得;右侧时,由
可得关于m的方程,解之可得;右侧时,由![]() 知
知![]() 、
、![]() 、
、![]() ,利用勾股定理求解可得.
,利用勾股定理求解可得.![]() 作
作![]() 于点G,延长GD交BE于点H,由
于点G,延长GD交BE于点H,由![]() ≌
≌![]() 知
知![]() ,据此可得
,据此可得 ,再分点D在矩形内部和外部的情况求解可得.
,再分点D在矩形内部和外部的情况求解可得.
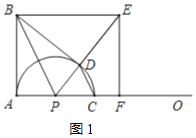
![]() 如图1,
如图1,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 、
、![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形ABEF是矩形,
四边形ABEF是矩形,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
解得:![]() ,
,
![]() 的长为10.
的长为10.
![]() 如图1,当点C在AF的左侧时,
如图1,当点C在AF的左侧时,
![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,由
中,由![]() 可得
可得![]() ,
,
解得:![]() 负值舍去
负值舍去![]() ;
;
如图2,当点C在AF的右侧时,
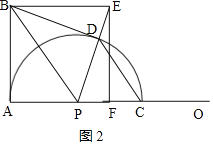
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,由
中,由![]() 可得
可得![]() ,
,
解得:![]() 负值舍去
负值舍去![]() ;
;
综上,m的值为![]() 或
或![]() ;
;
![]() 如图3,过点D作
如图3,过点D作![]() 于点G,延长GD交BE于点H,
于点G,延长GD交BE于点H,
![]() ≌
≌![]() ,
,
![]() ,
,
又![]() ,且
,且![]() ,
,
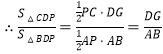 ,
,
当点D在矩形ABEF的内部时,
由![]() 可设
可设![]() 、
、![]() ,
,
则![]() ,
,
![]() ,
,
则![]() ;
;
如图4,当点D在矩形ABEF的外部时,

由![]() 可设
可设![]() 、
、![]() ,
,
则![]() ,
,
![]() ,
,
则![]() ,
,
综上,![]() 与
与![]() 面积比为
面积比为![]() 或
或![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知点![]() 分别在菱形
分别在菱形![]() 的边
的边![]() 上滑动(点
上滑动(点![]() 不与
不与![]() 重合),且
重合),且![]() .
.
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() 与
与![]() 不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;
不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;
(3)如图3,若![]() ,请直接写出四边形
,请直接写出四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
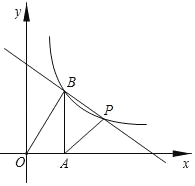
【题目】如图,在平面直角坐标系中,函数y=![]() 的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
(1)求k的值和点B的坐标.
(2)求直线BP的解析式.
(3)直接写出在第一象限内,使反比例函数大于一次函数的x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图.
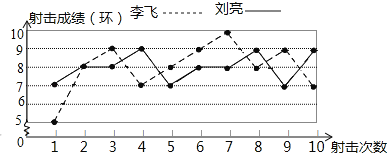
根据图所提供的信息,若要推荐一位成绩较稳定的选手去参赛,应推荐( )
A. 李飞或刘亮 B. 李飞 C. 刘亮 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是 ( )
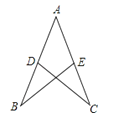
A. AB=AC B. ∠ADC=∠AEB C. ∠B=∠C D. BE=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的三个顶点分别为
的三个顶点分别为![]() ,
,![]() ,
,![]() .
.
![]() 把
把![]() 向上平移
向上平移![]() 个单位后得到
个单位后得到![]() ,请画出
,请画出![]() ;
;
![]() 已知点
已知点![]() 与点
与点![]() 关于直线
关于直线![]() 成轴对称,请画出直线
成轴对称,请画出直线![]() 及
及![]() 关于直线
关于直线![]() 对称的
对称的![]() .
.
![]() 在
在![]() 轴上存在一点
轴上存在一点![]() ,满足点
,满足点![]() 到点
到点![]() 与点
与点![]() 距离之和最小,请直接写出
距离之和最小,请直接写出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:h),随机调査了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
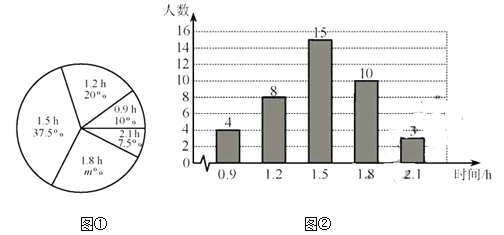
(Ⅰ)本次接受调查的初中学生人数为___________,图①中m的值为_____________;
(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有800名初中学生,估计该校每天在校体育活动时间大于1h的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB、AC上.

(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com