
(本题满分10分)如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,若AB=17,BD=12,
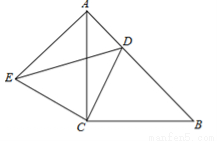
(1)求证:△BCD≌△ACE;
(2)求DE的长度.
(1)证明见试题解析;(2)13.
【解析】
试题分析:(1)根据等腰直角三角形得出AC=BC,CE=CD,∠ACB=∠ECD=90°,求出∠BCD=∠ACE,根据SAS推出△BCD≌△ACE即可.
(2)求出AD=5,根据全等得出AE=BD=12,在Rt△AED中,由勾股定理求出DE即可.
试题解析:(1)∵△ACB与△ECD都是等腰直角三角形,∴AC=BC,CE=CD,
∵∠ACB=∠ECD=90°,∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,∴∠BCD=∠ACE,
在△BCD和△ACE中,∵BC=AC,∠BCD=∠ACE,CD=CE,∴△BCD≌△ACE(SAS).
(2)由(1)知△BCD≌△ACE,则∠DBC=∠EAC,
∵∠CAD+∠DBC=90°,∴∠EAC+∠CAD=90°,即∠EAD=90°
∵AB=17,BD=12,∴AD=17﹣12=5,
∵△BCD≌△ACE,∴AE=BD=12,
在Rt△AED中,由勾股定理得:DE=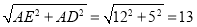 .
.
考点:1.全等三角形的判定与性质;2.等腰直角三角形.


科目:初中数学 来源:2014-2015学年江苏省江阴市青阳片九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分10分)类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.

原题:如图1,在□ABCD中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若 ,求
,求 的值.
的值.
(1)尝试探究
在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 , 的值是 .
的值是 .
(2)类比延伸
如图2,在原题的条件下,若 则
则 的值是 (用含
的值是 (用含 的代数式表示),试写出解答过程.
的代数式表示),试写出解答过程.
(3)拓展迁移
如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若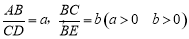 ,则
,则 的值是 (用a,b含的代数式表示).
的值是 (用a,b含的代数式表示).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省附中八年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,若D为△ABC的边BC上一点,且AD=BD,AB=AC=CD,则∠BAC= .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省附中八年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分8分)在如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两个格点,若C也是图中的格点,且使得△ABC为等腰三角形,在网格中画出所有符合条件的点C.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省附中八年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分12分)问题解决
(1)如图(1),将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN.当 时,求
时,求 的值.
的值.

类比归纳
(2)在图(1)中,若 则
则 的值等于 ;若
的值等于 ;若 则
则 的值等于 ;若
的值等于 ;若 (
( 为整数),则
为整数),则 的值等于 .(用含
的值等于 .(用含 的式子表示)
的式子表示)
联系拓广
(3)如图(2),将矩形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN,设 (
( ),
), ,则
,则 的值等于 .
的值等于 .
(用含 的式子表示)
的式子表示)


查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市高新区九年级上学期期中联考数学试卷(解析版) 题型:填空题
如图,□ABCD中,E是CD的延长线上一点,B与AD交于点F,CD=2DE.若△DEF的面积为a,则□ABCD的面积为 .(用a的代数式表示)

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省靖江市共同体九年级上学期期中考试数学试卷(解析版) 题型:选择题
在中,若tanA=1,sinB= ,则⊿ABC的形状是( )
,则⊿ABC的形状是( )
A.等腰三角形 B.等腰直角三角形 C.直角三角形 D.一般锐角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com