
(本题满分12分)问题解决
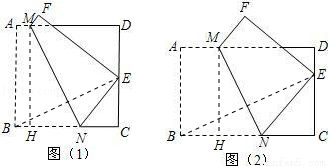
(1)如图(1),将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN.当 时,求
时,求 的值.
的值.

类比归纳
(2)在图(1)中,若 则
则 的值等于 ;若
的值等于 ;若 则
则 的值等于 ;若
的值等于 ;若 (
( 为整数),则
为整数),则 的值等于 .(用含
的值等于 .(用含 的式子表示)
的式子表示)
联系拓广
(3)如图(2),将矩形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN,设 (
( ),
), ,则
,则 的值等于 .
的值等于 .
(用含 的式子表示)
的式子表示)


(1)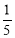 ;(2)
;(2)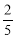 ,
,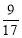 ,
,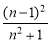 ;(3)
;(3)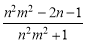 .
.
【解析】
试题分析:如图(1﹣1),连接BM,EM,BE.由题设,得四边形ABNM和四边形FENM关于直线MN对称.由轴对称的性质知MN垂直平分BE.有BM=EM,BN=EN.由于四边形ABCD是正方形,则有∠A=∠D=∠C=90°,设AB=BC=CD=DA=2.由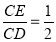 得,CE=DE=1;设BN=x,则NE=x,NC=2﹣x.在Rt△CNE中,由勾股定理知NE2=CN2+CE2.即x2=(2﹣x)2+12可解得x的值,从而得以BN的值,在Rt△ABM和在Rt△DEM中,由勾股定理知AM2+AB2=BM2,DM2+DE2=EM2,有AM2+AB2=DM2+DE2.
得,CE=DE=1;设BN=x,则NE=x,NC=2﹣x.在Rt△CNE中,由勾股定理知NE2=CN2+CE2.即x2=(2﹣x)2+12可解得x的值,从而得以BN的值,在Rt△ABM和在Rt△DEM中,由勾股定理知AM2+AB2=BM2,DM2+DE2=EM2,有AM2+AB2=DM2+DE2.
设AM=y,则DM=2﹣y,y2+22=(2﹣y)2+12可求得y的值,得到AM的值从而得到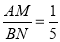 ;
;
(2)先算当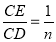 (
(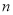 为整数)时,
为整数)时, 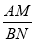 的值,然后代入即可得到n=3,n=4时,
的值,然后代入即可得到n=3,n=4时,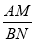 的值;
的值;
(3)先用含m,n代数式表示出AM,BN,然后求出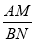 的值即可.
的值即可.
试题解析:(1)如图(1﹣1),连接BM,EM,BE.
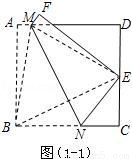
由题设,得四边形ABNM和四边形FENM关于直线MN对称,∴MN垂直平分BE,
∴BM=EM,BN=EN,
∵四边形ABCD是正方形,∴∠A=∠D=∠C=90°,设AB=BC=CD=DA=2.
∵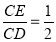 ,∴CE=DE=1.
,∴CE=DE=1.
设BN=x,则NE=x,NC=2﹣x.在Rt△CNE中,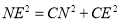 .
.
∴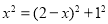 ,解得
,解得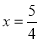 ,即BN=
,即BN=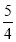 .
.
在Rt△ABM和在Rt△DEM中,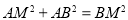 ,
, ,
,
∴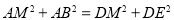 .
.
设AM=y,则DM=2﹣y,
∴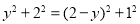 ,解得:
,解得: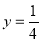 ,即AM=
,即AM=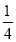 ,∴
,∴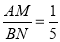 .
.
(2)如图1,当四边形ABCD为正方形时,连接BE,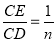 ,
,
不妨令CD=CB=n,则CE=1,设BN=x,则EN=x,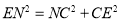 ,
,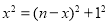 ,
,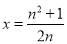 ;
;
作MH⊥BC于H,则MH=BC,
又点B,E关于MN对称,则MN⊥BE,∠EBC+∠BNM=90°;而∠NMH+∠BNM=90°,故∠EBC=∠NMH,则△EBC≌△NMH,
∴NH=EC=1,AM=BH=BN﹣NH=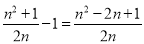 ,则:
,则: .
.
故当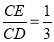 ,则
,则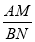 的值等于
的值等于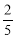 ;若
;若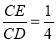 ,则
,则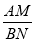 的值等于
的值等于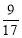 ;
;
(3)若四边形ABCD为矩形,连接BE,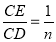 ,不妨令CD=n,则CE=1;
,不妨令CD=n,则CE=1;
又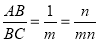 ,则BC=mn,同样的方法可求得:BN=
,则BC=mn,同样的方法可求得:BN=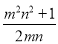 ,
,
BE⊥MN,易证得:△MHN∽△BCE.故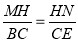 ,
,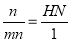 ,
,
HN=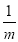 ,故AM=BH=BN﹣HN=
,故AM=BH=BN﹣HN=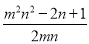 ,
,
故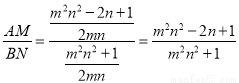 .
.
考点:1.翻折变换(折叠问题);2.矩形的性质;3.正方形的性质.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源:2014-2015学年江苏省泰兴市七年级上学期期中考试数学试卷(解析版) 题型:选择题
下列轴对称图形中,可以用没有刻度的直尺画出对称轴的有( )

A.1个 B.2个 C.3个 D,4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰兴市七年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题8分) 已知:D为△ABC所在平面内一点,且DB=DC,DE⊥AB,DF⊥AC,垂足分别是E、F,DE=DF.
(1)当点D在BC边上时(如图),判断△ABC的形状(直接写出答案);

(2)当点D在△ABC内部时,(1)中的结论是否一定成立?若成立,请证明;若不成立,请举出反例(画图说明).
(3)当点D在△ABC外部时,(1)中的结论是否一定成立?若成立,请证明;若不成立,请举出反例(画图说明).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省附中八年级上学期期中考试数学试卷(解析版) 题型:填空题
如图在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省附中八年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分10分)如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,若AB=17,BD=12,
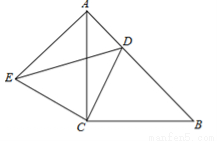
(1)求证:△BCD≌△ACE;
(2)求DE的长度.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市高新区九年级上学期期中联考数学试卷(解析版) 题型:解答题
(本题满分6分)已知关于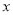 的方程
的方程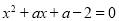 .
.
(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论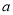 取何实数,该方程都有两个不相等的实数根.
取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市高新区九年级上学期期中联考数学试卷(解析版) 题型:解答题
(本题满分7分)如图,已知二次函数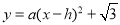 的图象经过原点0(0,0),A(2,0).
的图象经过原点0(0,0),A(2,0).

(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA',试判断点A'是否在该函数图象上?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省上学期九年级第一次段考数学试卷(解析版) 题型:选择题
用配方法解方程 ,应把方程的两边同时( )
,应把方程的两边同时( )
A.加上 B.加上
B.加上 C.减去
C.减去 D.减去
D.减去
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com