
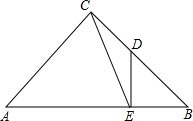
 如图,已知△ABC是等腰直角三角形,∠ACB=90°,过BC的中点D作DE⊥AB于E,连结CE,求sin∠ACE=$\frac{3\sqrt{10}}{10}$.
如图,已知△ABC是等腰直角三角形,∠ACB=90°,过BC的中点D作DE⊥AB于E,连结CE,求sin∠ACE=$\frac{3\sqrt{10}}{10}$. 分析 要求sin∠ACE的值,关键是构造直角三角形,作EF⊥AC,只要求出EF和EC的长即可,根据题目中的条件可以表示出它们的长,本题得以解决.
解答 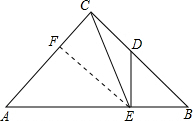 解:作EF⊥AC于点F,如右图所示,
解:作EF⊥AC于点F,如右图所示,
设AC=BC=2a,
∵△ABC是等腰直角三角形,∠ACB=90°,过BC的中点D作DE⊥AB于E,
∴∠ACB=90°,∠B=∠A=45°,CD=BD=a,∠DEB=90°,
∴AB=$2\sqrt{2}a$,BE=$\frac{\sqrt{2}a}{2}$,
∴AE=$\frac{3\sqrt{2}a}{2}$,
∵EF⊥AC,BC⊥AC,
∴△AFE∽△ACB,
∴$\frac{EF}{BC}=\frac{AE}{AB}=\frac{AF}{AC}$,
解得,EF=$\frac{3a}{2}$,AF=$\frac{3a}{2}$,
∴CF=$\frac{a}{2}$,
∴EC=$\frac{\sqrt{10}a}{2}$,
∴sin∠ACE=$\frac{EF}{CE}=\frac{\frac{3a}{2}}{\frac{\sqrt{10}a}{2}}$=$\frac{3\sqrt{10}}{10}$,
故答案为:$\frac{3\sqrt{10}}{10}$.
点评 本题考查解直角三角形、等腰直角三角形,解题的关键是明确题意,构造直角三角形,找出所求问题需要的条件.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:选择题
| A. | 400 | B. | 401 | C. | 402 | D. | 403 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
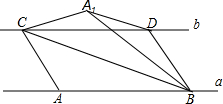 如图,直线a与b平行,点A、B是直线a上两个定点,点CD在直线b上运动(点C在点D的左侧),AB=CD=4cm,a、b之间的距离为$\sqrt{3}$cm,连接AC、BD、BC,把△ABC沿BC折叠得△A1BC.
如图,直线a与b平行,点A、B是直线a上两个定点,点CD在直线b上运动(点C在点D的左侧),AB=CD=4cm,a、b之间的距离为$\sqrt{3}$cm,连接AC、BD、BC,把△ABC沿BC折叠得△A1BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
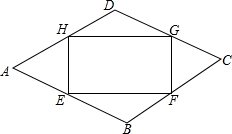 如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,已知∠A=60°.
如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,已知∠A=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com