

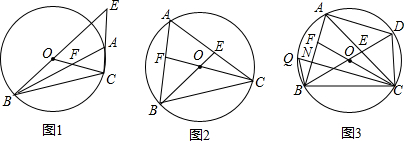
ЗжЮі ЃЈ1ЃЉгЩЫФБпаЮABCDЪЧОиаЮКЭШ§НЧАхЕФЬиЕуЃЌЕУЕНOB=ODЃЌЁЯDON=90ЁуРћгУЙДЙЩЖЈРэЃЌМДПЩЃЛ
ЃЈ2ЃЉгЩЫФБпаЮABCDЮЊОиаЮКЭШ§НЧАхЕФЬиЕуЃЌЕУГіНсТлЃЌХаЖЯГіЁїBONЁеЁїDOPЃЌдйРћгУЙДЙЩЖЈРэЃЌМДПЩЃЛ
ЃЈ3ЃЉгЩОиаЮКЭШ§НЧАхЕФЬиЕувдМАа§зЊЕФаджЪЕУЕНЃЌMP=MNЃЌРћгУЙДЙЩЖЈРэЃЌШЛКѓгУCM+CN=$\frac{44}{5}$ЃЌМДПЩЃЎ
НтД№ ЃЈ1ЃЉжЄУїЃКШчЭМЂйЃЌСЌНгDNЃЌ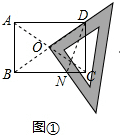
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрOB=ODЃЌ
ЁпЁЯDON=90ЁуЃЌ
ЁрBN=DNЃЌ
ЁпЁЯBCD=90ЁуЃЌ
ЁрDN2=CD2+CN2ЃЌ
ЁрBN2=CD2+CN2ЃЛ
ШчЭМЂлЃЌ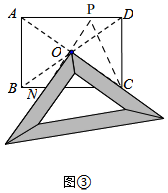
бгГЄNOНЛADгкPЃЌ
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрOD=OBЃЌADЁЮBCЃЌ
ЁрЁЯDPO=ЁЯBNOЃЌЁЯPDO=ЁЯNBOЃЌ
дкЁїBONКЭЁїDOPжа
$\left\{\begin{array}{l}{ЁЯNBO=ЁЯPDO}\\{ЁЯBNO=ЁЯDPO}\\{OB=OD}\end{array}\right.$ЃЌ
ЁрЁїBONЁеЁїDOPЃЌ
ЁрON=OPЃЌBN=PDЃЌ
ЁпOCЁЭDPЃЌ
ЁрCN=CPЃЌ
ИљОнЙДЙЩЖЈРэЕУЃЌCP2=DP2+CD2ЃЌ
ЁрCN2=BN2+CD2
ЙЪД№АИЮЊCN2=CD2+BN2ЃЛ
ЃЈ2ЃЉжЄУїЃКШчЭМЂкЃЌбгГЄNOНЛADгкЕуPЃЌСЌНгPMЃЌMNЃЌ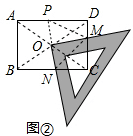
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрOD=OBЃЌADЁЮBCЃЌ
ЁрЁЯDPO=ЁЯBNOЃЌЁЯPDO=ЁЯNBOЃЌ
дкЁїBONКЭЁїDOPжа
$\left\{\begin{array}{l}{ЁЯNBO=ЁЯPDO}\\{ЁЯBNO=ЁЯDPO}\\{OB=OD}\end{array}\right.$ЃЌ
ЁрЁїBONЁеЁїDOPЃЌ
ЁрON=OPЃЌBN=PDЃЌ
ЁпЁЯMON=90ЁуЃЌ
ЁрPM=MNЃЌ
ЁпЁЯADC=ЁЯBCD=90ЁуЃЌ
ЁрPM2=PD2+DM2ЃЌMN2=CM2+CN2ЃЌ
ЁрPD2+DM2=CM2+CN2ЃЌ
ЁрBN2+DM2=CM2+CN2ЃЎ
ЃЈ3ЃЉШчЭМЂлЃЌ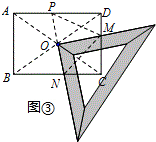
бгГЄNOНЛADгкЕуPЃЌСЌНгMNЃЌMPЃЌ
ЁпOЮЊОиаЮABCDЕФЖдНЧЯпЕФНЛЕуЃЌ
ЁргЩа§зЊПЩЕУЃЌBN=DPЃЌOP=ONЃЌ
ЁрOMДЙжБЦНЗжPNЃЌ
ЁрMP=MNЃЌ
дкRtЁїMDPжаЃЌMP2=DP2+DM2ЃЌ
дкRtЁїMCNжаЃЌMM2=CN2+CM2ЃЌ
ЁпMP=MNЃЌBN=DPЃЌ
ЁрBN2+DM2=CN2+CM2ЃЌ
ЩшDM=xЃЌCN=yЃЌ
ЁрCM=8-xЃЌBN=10-yЃЌ
ЁрЃЈ10-yЃЉ2+x2=y2+ЃЈ8-xЃЉ2ЃЌ
Ёрy=$\frac{4}{5}$x+$\frac{9}{5}$ЃЌ
ЁрCM+CN=8-x+y=8-x+$\frac{4}{5}$x+$\frac{9}{5}$=$\frac{49}{5}$-$\frac{1}{5}$xЃЌ
ЁпCM+CN=$\frac{44}{5}$ЃЌ
Ёр$\frac{49}{5}$-$\frac{1}{5}$x=$\frac{44}{5}$ЃЌ
Ёрx=5ЃЌ
ЁрЕБDM=5ЪБЃЌCM+CN=$\frac{44}{5}$ЃЎ
ЕуЦР ДЫЬтЪЧМИКЮБфЛЛзлКЯЬтЃЌжївЊПМВщСЫа§зЊЕФаджЪЃЌОиаЮЕФаджЪЃЌЙДЙЩЖЈРэЃЌгУЙДЙЩЖЈРэЕУЕНPM2=PD2+DM2ЃЌMN2=CM2+CN2зЊЛЏГіBN2+DM2=CM2+CN2ЪЧНтБОЬтЕФЙиМќЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
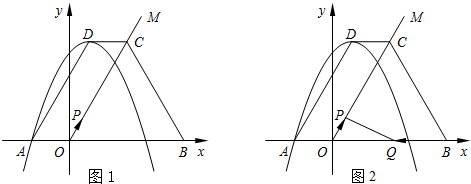
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
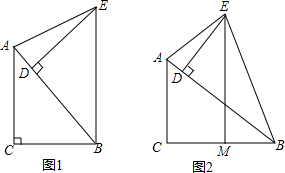
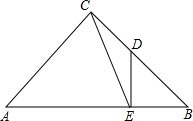 ШчЭМЃЌвбжЊЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯACB=90ЁуЃЌЙ§BCЕФжаЕуDзїDEЁЭABгкEЃЌСЌНсCEЃЌЧѓsinЁЯACE=$\frac{3\sqrt{10}}{10}$ЃЎ
ШчЭМЃЌвбжЊЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯACB=90ЁуЃЌЙ§BCЕФжаЕуDзїDEЁЭABгкEЃЌСЌНсCEЃЌЧѓsinЁЯACE=$\frac{3\sqrt{10}}{10}$ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com