
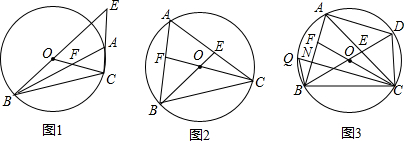
分析 (1)如图1,根据三角形外角的性质可得∠BEC+∠ABE=60°,根据三角形内角和定理可得∠BFO+∠ABE=60°,根据等量代换即可解决问题;
(2)在OF上取一点G,使得OG=OE,如图2,易证△GOB≌△EOC,则有BG=CE,∠BGO=∠OEC.要证BF=CE,只需证BF=BG即可;
(3)如图3,根据圆内接四边形对角互补可得∠ABC+∠ADC=180°,结合条件可得∠QBA=∠DBC=30°,从而可得到∠QNB=90°(即CQ⊥AB).在Rt△BCD中运用勾股定理可求出BC,在Rt△BNC中运用勾股定理可求出NC,然后在Rt△ANC中运用三角函数和勾股定理可求出AN和AC,要求AE,只需求出EC,由于BF=EC,只需求出BF,由于AF已知,只需求出AB即可.
解答 解:(1)如图1,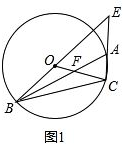
∵∠BAC=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×120°=60°,
∴∠BEC+∠ABE=∠BAC=60°.
∵∠BFO+∠ABE+∠BOC=180°,
∴∠BFO+∠ABE=60°,
∴∠BEC=∠BFO;
(2)在OF上取一点G,使得OG=OE,如图2,
在△GOB和△EOC中,
$\left\{\begin{array}{l}{OG=OE}\\{∠GOB=∠EOC}\\{OB=OC}\end{array}\right.$,
∴△GOB≌△EOC,
∴BG=CE,∠BGO=∠OEC.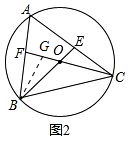
∵∠BAC=$\frac{1}{2}$∠BOC=60°,∠EOF=∠BOC=120°,
∠BAC+∠AFO+∠EOF+∠AEO=360°,
∴∠AFO+∠AEO=180°.
∵∠OEC+∠AEO=180°,
∴∠AFO=∠OEC,
∴∠AFO=∠OGB.
∵∠AFO+∠BFG=180°,∠BGF+∠OGB=180°,
∴∠BFG=∠BGF,
∴BF=BG,
∴BF=CE;
(3)如图3,
∵∠QBD+∠ADC=180°,∠ABC+∠ADC=180°,
∴∠QBD=∠ABC,
∴∠QBA=∠DBC.
∵OB=OC,∠BOC=120°,
∴∠OBC=∠OCB=30°,
∴∠QBA=30°.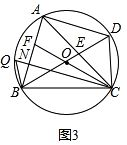
∵∠BQC=∠BAC=60°,
∴∠QNB=90°,即CQ⊥AB.
∵BD是⊙O的直径,
∴∠BCD=90°.
∵∠BDC=∠BAC=60°,
∴BC=BD•sin∠BDC=2×$\frac{7\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$=7.
在Rt△BNC中,
NC=$\sqrt{B{C}^{2}-B{N}^{2}}$=$\sqrt{49-1}$=4$\sqrt{3}$.
在Rt△ANC中,
NC=AN•tan60°=$\sqrt{3}$AN=4$\sqrt{3}$,
∴AN=4,AC=$\sqrt{A{N}^{2}+N{C}^{2}}$=8,
∴AB=AN+BN=4+1=5,
∴BF=AB-AF=5-$\frac{6}{5}$=$\frac{19}{5}$,
∴EC=BF=$\frac{19}{5}$,
∴AE=AC-EC=8-$\frac{19}{5}$=$\frac{21}{5}$.
点评 本题主要考查了三角形外角的性质、多边形内角和定理、等量代换、全等三角形的判定与性质、圆内接四边形对角互补、圆周角定理、三角函数、勾股定理等知识,构造三角形全等是解决第(2)小题的关键,证到CQ⊥AB并利用(2)的结论BF=CE是解决第(3)小题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
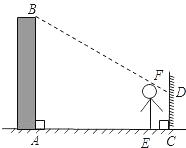 小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如图,小明边移动边观察,发现站在点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同,此时,小明测得自己落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上),已知小明的身高EF是1.7m,请你帮小明求出楼高AB.(结果精确到0.1m).
小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如图,小明边移动边观察,发现站在点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同,此时,小明测得自己落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上),已知小明的身高EF是1.7m,请你帮小明求出楼高AB.(结果精确到0.1m).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com