
【题目】(1)如图1,正方形ABCD和正方形DEFG,G在AD边上,E在CD的延长线上.求证:AE=CG,AE⊥CG;
(2)如图2,若将图1中的正方形DEFG绕点D顺时针旋转角度θ(0°<θ<90°),此时AE=CG还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)如图3,当正方形DEFG绕点D顺时针旋转45°时,延长CG交AE于点H,当AD=4,DG=![]() 时,求线段CH的长.
时,求线段CH的长.

【答案】(1)(2)见解析;(3)![]() .
.
【解析】试题分析:(1)先判断出△ADE≌△CDG,然后用互余判断出垂直;
(2)先判断出△ADE≌△CDG,然后用互余判断出垂直;
(3)先判断出△ADE≌△CDG,然后用互余判断出垂直,然后用勾股定理计算出CM,AM最后用相似即可.
试题解析:(1)在△ADE和△CDG中,
DE=DG,∠ADE=∠CDG,AD=CD,
∴△ADE≌△CDG,
∴AE=CG,∠AED=∠CGD,
∵∠DCG+∠CGD=90°,
∴∠DCG+∠AED=90°,
∴AE⊥CG.
(2)∵∠CDG+∠ADG=90°,∠ADE+∠ADG=90°,
∴∠CDG=∠ADE
在△ADE和△CDG中,
DE=DG,∠ADE=∠CDG,AD=CD,
∴△ADE≌△CDG,
∴AE=CG,∠AED=∠CGD,
∵∠DCG+∠CGD=90°,
∴∠DCG+∠AED=90°,
∴AE⊥CG.
(3)如图,
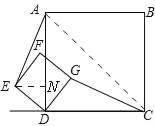
过点E作AD的垂线,垂足为N,连接AC,
在△ADE和△CDG中,
DE=DG,∠ADE=∠CDG,AD=CD,
∴△ADE≌△CDG,
∴∠EAD=∠DCM
∴tan∠DCM=![]() ,
,
∴DM=![]() CD=
CD=![]()
∴CM=![]() =
=![]() ,AM=AD﹣DM=
,AM=AD﹣DM=![]()
∵△CMD∽△AMH,
∴![]() ,
,
∴AH=![]() ,
,
∴CH=![]() =
=![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.

(1)学校采用的调查方式是 ;学校共选取了 名学生;
(2)补全统计图中的数据:条形统计图中羽毛球 人、乒乓球 人、其他 人、扇形统计图中其他 %;
(3)该校共有1200名学生,请估计喜欢“乒乓球”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).
(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD
面上的概率为0.75;若存在,指出其中的一种平移方式;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顺次连结一四边形各边的中点,若所得的四边形是一个菱形,则原四边形一定是( ).
A.矩形B.对角线相互垂直的四边形
C.平行四边形D.对角线相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲容器中装有浓度为a的果汁![]() ,乙容器中装有浓度为b的果汁
,乙容器中装有浓度为b的果汁![]() ,两个容器都倒出m kg,把甲容器倒出的果汁混入乙容器,把乙容器倒出的果汁混入甲容器,混合后,两容器内的果汁浓度相同,则m的值为_________.
,两个容器都倒出m kg,把甲容器倒出的果汁混入乙容器,把乙容器倒出的果汁混入甲容器,混合后,两容器内的果汁浓度相同,则m的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】喜迎新中国70华诞,感受祖国70年沧桑巨变,70年壮丽辉煌,西大附中开展“祖国,我为你骄傲”的歌唱比赛,为了筹集歌唱比赛的演出服装资金,初二年级从批发市场购进![]() 、
、![]() 两种材料用于手工制作,进行“爱心义卖”.若每个
两种材料用于手工制作,进行“爱心义卖”.若每个![]() 种材料的进价比每个
种材料的进价比每个![]() 种材料的进价少2元,且用160元购进
种材料的进价少2元,且用160元购进![]() 种材料的数量与用200元购进
种材料的数量与用200元购进![]() 种材料的数量相等.
种材料的数量相等.
(1)求![]() 、
、![]() 两种材料的进价分别为多少元?
两种材料的进价分别为多少元?
(2)同学们齐心协力、大胆创新制作出了新颖别致的甲、乙两种手工艺品共56个,乙的数量比甲的数量的两倍还多,但多的个数不超过2个,甲的售价是24元/个,乙的售价是30元/个,为了使利润不低于1040元,有几种制作方案,哪种利润方案最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com