
【题目】O为直线DA上一点,OB⊥OF,EO是∠AOB的平分线.
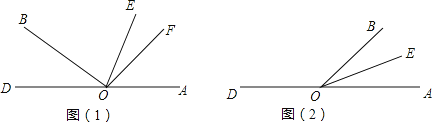
(1)如图(1),若∠AOB=130°,求∠EOF的度数;
(2)若∠AOB=α,90°<α<180°,求∠EOF的度数;
(3)若∠AOB=α,0°<α<90°,请在图(2)中画出射线OF,使得(2)中∠EOF的结果仍然成立.
【答案】(1)25°;(2)90![]() ;(3)90
;(3)90![]() .
.
【解析】
试题分析:(1)首先利用角平分线的定义可得∠AOE的度数,由垂直的定义得∠BOF=90°,易得∠AOF,可得∠EOF;
(2)首先利用角平分线的定义可得∠AOE=![]() ,由垂直的定义得∠BOF=90°,易得∠AOF=α﹣90°,可得∠EOF;
,由垂直的定义得∠BOF=90°,易得∠AOF=α﹣90°,可得∠EOF;
(3)根据题意OB⊥OF,使得(2)中∠EOF的结果仍然成立,画出射线OF即可,再结合图形同理(2)可得结果.
解:(1)∵∠AOB=130°,EO是∠AOB的平分线,
∴![]() =65°,
=65°,
∵OB⊥OF,
∴∠BOF=90°,
∴∠AOF=∠AOB﹣∠BOF=130°﹣90°=40°,
∴∠EOF=∠AOE﹣∠AOF=65°﹣40°=25°;
(2)∵∠AOB=α,90°<α<180°,EO是∠AOB的平分线,
∴∠AOE=![]() ,
,
∵∠BOF=90°,
∴∠AOF=α﹣90°,
∴∠EOF=∠AOE﹣∠AOF=![]() ﹣(α﹣90°)=90
﹣(α﹣90°)=90![]() ;
;
(3)如图,∵∠AOB=α,0°<α<90°,
∴∠BOE=∠AOE=![]() ,
,
∵∠BOF=90°,
∴∠EOF=∠BOF﹣∠BOE=90![]() .
.



科目:初中数学 来源: 题型:
【题目】(1)已知x2+x﹣5=0,求代数式(x﹣1)2﹣x(x﹣3)+(x+2)(x﹣2)的值
(2)先化简(1﹣![]() )÷
)÷![]() ,再从﹣2≤a≤2中选一个你认为合适的整数作为a的值代入求值.
,再从﹣2≤a≤2中选一个你认为合适的整数作为a的值代入求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O是坐标原点,B、C两点的坐标分别为(3,﹣1)、(2,1).
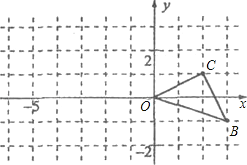
(1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)分别写出B、C两点的对应点B′、C′的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试通过画图来判定,下列说法正确的是( )
A. 一个直角三角形一定不是等腰三角形 B. 一个等腰三角形一定不是锐角三角形
C. 一个钝角三角形一定不是等腰三角形 D. 一个等边三角形一定不是钝角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小乐的数学积累本上有这样一道题:
解方程:![]() ﹣
﹣![]() =1
=1
解:去分母,得6(2x+1)﹣(5x﹣1)=6…第一步
去括号,得4x+2﹣5x﹣1=6…第二步
移向、合并同类项,得x=5…第三步
方程两边同除以﹣1,得x=﹣5…第四步
在题后的反思中看,小郑总结到:解一元一次方程的一般步骤都知道,却没有掌握好,因此解题时有一步出现了错误…
小乐的解法从第 步开始出现错误,然后,请你自己细心地解下面的方程:
2﹣![]() (x+2)=
(x+2)=![]() (x﹣1)
(x﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:
①(﹣11)+5
②5﹣(﹣![]() )+(﹣7)﹣
)+(﹣7)﹣![]()
③(﹣3)2+(﹣16)÷[(﹣![]() )÷(﹣
)÷(﹣![]() )]
)]
(2)化简并求值
3(x2y+xy2)﹣2(xy+xy2)﹣![]() x2y,其中x是绝对值等于2的负数,y是最大的负整数.
x2y,其中x是绝对值等于2的负数,y是最大的负整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据道路交通管理条例的规定,在某段笔直的公路l上行驶的车辆,限速60千米/时.已知测速点M到测速区间的端点A,B的距离分别为50米、34米,M距公路l的距离(即MN的长)为30米.现测得一辆汽车从A到B所用的时间为5秒,通过计算判断此车是否超速.
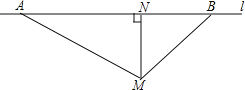
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com