
分析 去分母、去括号、移项、合并同类项、系数化成1即可求得不等式的解集,然后确定解集中的非负整数解即可.
解答 解:去分母,得3(x-2)≤2(7-x),
去括号,得3x-6≤14-2x,
移项,得3x+2x≤14+6,
合并同类项,得5x≤20,
系数化成1得x≤4.
则非负整数解是:0、1、2、3、4.
点评 本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.
解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
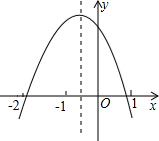 已知二次函数y=ax2+bx+c的图象如图所示,下列结论,错误的是( )
已知二次函数y=ax2+bx+c的图象如图所示,下列结论,错误的是( )| A. | abc>0 | B. | 2a-b<0 | C. | 4a-2b+c<0 | D. | (a+c)2>b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠B=90°,AB=12mm,AC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点D从点A开始沿边AC以4mm/s的速度移动.过点D作QD∥AB交BC于Q,设P,D两点从点A同时出发,运动时间为ts.
如图,在△ABC中,∠B=90°,AB=12mm,AC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点D从点A开始沿边AC以4mm/s的速度移动.过点D作QD∥AB交BC于Q,设P,D两点从点A同时出发,运动时间为ts.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com