
【题目】(12分)如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.
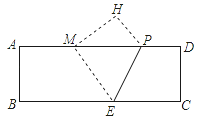
(1)求MP的值;
(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?
(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)
【答案】(1)5;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)由折叠的性质和矩形性质以得PD=PH=3,CD=MH=4,∠H=∠D=90°,利用勾股定理可计算出MP的长;
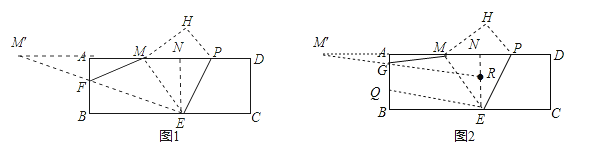
(2)如图1,作点M关于AB的对称点M′,连接M′E交AB于点F,利用两点之间线段最短可得点F即为所求,过点E作EN⊥AD,垂足为N,则AM=AD﹣MP﹣PD=4,所以AM=AM′=4,再证明ME=MP=5,利用勾股定理计算出MN=3, NM′=11,得出△AFM′∽△NEM′,利用相似比即可计算出AF;
(3)如图2,由(2)知点M′是点M关于AB的对称点,在EN上截取ER=2,连接M′R交AB于点G,再过点E作EQ∥RG,交AB于点Q,易得QE=GR,而GM=GM′,于是MG+QE=M′R,利用两点之间线段最短可得此时MG+EQ最小,于是四边形MEQG的周长最小,在Rt△M′RN中,利用勾股定理计算出M′R得出,从而得到四边形MEQG的最小周长值.
试题解析:(1)∵四边形ABCD为矩形,∴CD=AB=4,∠D=90°,∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,∴PD=PH=3,CD=MH=4,∠H=∠D=90°,∴MP=![]() =5;
=5;
(2)如图1,作点M关于AB的对称点M′,连接M′E交AB于点F,则点F即为所求,过点E作EN⊥AD,垂足为N,∵AM=AD﹣MP﹣PD=12﹣5﹣3=4,∴AM=AM′=4,∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,∴∠CEP=∠MEP,而∠CEP=∠MPE,∴∠MEP=∠MPE,∴ME=MP=5,在Rt△ENM中,MN=![]() =
=![]() =3,∴NM′=11,∵AF∥ME,∴△AFM′∽△NEM′,∴
=3,∴NM′=11,∵AF∥ME,∴△AFM′∽△NEM′,∴![]() ,即
,即![]() ,解得AF=
,解得AF=![]() ,即AF=
,即AF=![]() 时,△MEF的周长最小;
时,△MEF的周长最小;
(3)如图2,由(2)知点M′是点M关于AB的对称点,在EN上截取ER=2,连接M′R交AB于点G,再过点E作EQ∥RG,交AB于点Q,∵ER=GQ,ER∥GQ,∴四边形ERGQ是平行四边形,∴QE=GR,∵GM=GM′,∴MG+QE=GM′+GR=M′R,此时MG+EQ最小,四边形MEQG的周长最小,在Rt△M′RN中,NR=4﹣2=2,M′R=![]() =
=![]() ,∵ME=5,GQ=2,∴四边形MEQG的最小周长值是
,∵ME=5,GQ=2,∴四边形MEQG的最小周长值是![]() .
.


科目:初中数学 来源: 题型:
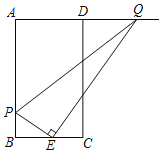
【题目】如图,在矩形ABCD中,![]() ,
,![]() ,点E是边BC的中点
,点E是边BC的中点![]() 动点P从点A出发,沿着AB运动到点B停止,速度为每秒钟1个单位长度,连接PE,过点E作PE的垂线交射线AD与点Q,连接PQ,设点P的运动时间为t秒.
动点P从点A出发,沿着AB运动到点B停止,速度为每秒钟1个单位长度,连接PE,过点E作PE的垂线交射线AD与点Q,连接PQ,设点P的运动时间为t秒.
![]() 当
当![]() 时,
时,![]() ______;
______;
![]() 是否存在这样的t值,使
是否存在这样的t值,使![]() 为等腰直角三角形?若存在,求出相应的t值,若不存在,请说明理由;
为等腰直角三角形?若存在,求出相应的t值,若不存在,请说明理由;
![]() 当t为何值时,
当t为何值时,![]() 的面积等于10?
的面积等于10?
查看答案和解析>>
科目:初中数学 来源: 题型:
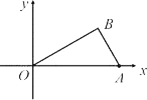
【题目】如图,已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
(1) 求点B的坐标;
(2) 若二次函数y=ax2+bx+c的图象经过A、B、O三点,求此二次函数的解析式;
(3) 在(2)中的二次函数图象的OB段(不包括点O、B)上,是否存在一点C,使得四边形ABCO的面积最大?若存在,求出这个最大值及此时点C的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列内容,并答题:我们知道,计算n边形的对角线条数公式为: ![]() n(n﹣3).
n(n﹣3).
如果一个n边形共有20条对角线,那么可以得到方程![]() n(n﹣3)=20 .
n(n﹣3)=20 .
整理得n2﹣3n﹣40=0;解得n=8或n=﹣5
∵n为大于等于3的整数,∴n=﹣5不合题意,舍去.
∴n=8,即多边形是八边形.
根据以上内容,问:
(1)若一个多边形共有14条对角线,求这个多边形的边数;
(2)A同学说:“我求得一个多边形共有10条对角线”,你认为A同学说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
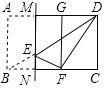
【题目】如图,在矩形ABCD中,AB:BC=3:5,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
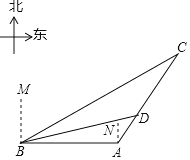
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
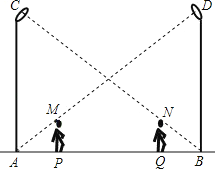
【题目】如图,王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行12m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.
(1)求两个路灯之间的距离;
(2)当王华同学走到路灯BD处时,他在路灯AC下的影子长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.
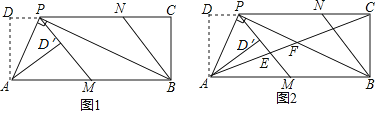
(1)求证:AD2=DPPC;
(2)请判断四边形PMBN的形状,并说明理由;
(3)如图2,连接AC,分别交PM,PB于点E,F.若![]() =
=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com