
ΓΨΧβΡΩΓΩΈ“Ο«÷ΣΒάΘ§‘ΎΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΚΆΚ§”–30ΓψΫ«ΒΡ÷±Ϋ«»ΐΫ«–Έ÷–Θ§»ΐ±Ώ÷°ΦδΒΡ±»άΐΙΊœΒΖ÷±π»γΆΦΥυ ΨΘΚ
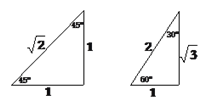
‘Ϋη÷ζ…œ ωΫα¬έΘ§ΙΙ‘λΆΦ–ΈΘ§ΫβΨωœ¬ΟφΒΡΈ ΧβΘΚ
»γΆΦ(1)Θ§“―÷ΣΓœACD=90ΓψΘ§MN «ΙΐΒψAΒΡ÷±œΏΘ§AC=DCΘ§DBΓΆMN”ΎΒψBΘ§
(1) «σ÷ΛΘΚ BD+AB=![]() CBΘΜ
CBΘΜ
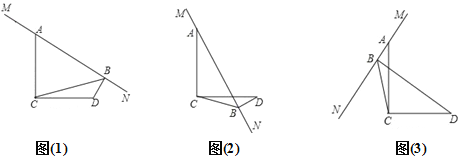
(2) Β±MN»ΤA–ΐΉΣΒΫ»γΆΦ(2)ΚΆΆΦ(3)ΝΫΗωΈΜ÷Ο ±Θ§BDΓΔABΓΔCB¬ζΉψ ≤Ο¥―υΙΊœΒ ΫΘ§«κ–¥≥ωΡψΒΡ≤¬œκΘ§≤ΔΕ‘ΆΦ(3)Ηχ”η÷ΛΟςΘΜ
(3) MN‘Ύ»ΤΒψA–ΐΉΣΙΐ≥Χ÷–Θ§Β±ΓœBCD=30ΓψΘ§BD=![]() ±Θ§‘ρCD=ΓΓ ΓΓΘ§CB=ΓΓ ΓΓΘ°
±Θ§‘ρCD=ΓΓ ΓΓΘ§CB=ΓΓ ΓΓΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©÷ΛΟςΦϊΫβΈωΘΜ(2) ![]() ;
; ![]() ΘΜ(3)2ΘΜ
ΘΜ(3)2ΘΜ ![]() .
.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΙΐΒψCΉςCEΓΆCB”ΎΒψCΘ§”κMNΫΜ”ΎΒψEΘ§÷ΛΟςΓςACEΓ’ΓςDCBΘ§‘ρΓςECBΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§Ψί¥ΥΦ¥Ω…ΒΟΒΫBE=![]() CBΘ§ΗυΨίBE=AE+ABΦ¥Ω…÷ΛΒΟΘΜ
CBΘ§ΗυΨίBE=AE+ABΦ¥Ω…÷ΛΒΟΘΜ
Θ®2Θ©ΙΐΒψCΉςCEΓΆCB”ΎΒψCΘ§”κMNΫΜ”ΎΒψEΘ§÷ΛΟςΓςACEΓ’ΓςDCBΘ§‘ρΓςECBΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§Ψί¥ΥΦ¥Ω…ΒΟΒΫBE=![]() CBΘ§ΗυΨίBE=AB-AEΦ¥Ω…÷ΛΒΟΘΜ
CBΘ§ΗυΨίBE=AB-AEΦ¥Ω…÷ΛΒΟΘΜ
Θ®3Θ©ΙΐΒψBΉςBHΓΆCD”ΎΒψHΘ§÷ΛΟςΓςBDH «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§«σΒΟDHΒΡ≥ΛΘ§‘Ύ÷±Ϋ«ΓςBCH÷–Θ§άϊ”Ο÷±Ϋ«»ΐΫ«–Έ÷–30ΓψΒΡ»ώΫ«ΥυΕ‘ΒΡ÷±Ϋ«±ΏΒ»”Ύ–±±ΏΒΡ“ΜΑκΘ§Φ¥Ω…«σΒΟΘ°
‘ΧβΫβΈωΘΚΘ®1Θ©ΙΐΒψCΉςCEΓΆCB”ΎΒψCΘ§”κMNΫΜ”ΎΒψEΘ§
ΓΏΓœACB+ΓœBCD=90Γψ,ΓœACB+ΓœACE=90ΓψΘ§
ΓύΓœBCD=ΓœACE.
ΓΏΥΡ±Ώ–ΈACDBΡΎΫ«ΚΆΈΣ360Γψ,
ΓύΓœBDC+ΓœCAB=180Γψ.
ΓΏΓœEAC+ΓœCAB=180ΓψΘ§
ΓύΓœEAC=ΓœBDC.
”÷ΓΏAC=DC,
ΓύΓςACEΓ’ΓςDCB,
ΓύAE=DB,CE=CB,
ΓύΓςECBΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ,
ΓύBE=![]() CB.
CB.
”÷ΓΏBE=AE+AB,
ΓύBE=BD+AB,
ΓύBD+AB=![]() CBΘΜ
CBΘΜ
(2)»γΆΦ(2) ABBD=![]() CB.άμ”…»γœ¬ΘΚ
CB.άμ”…»γœ¬ΘΚ

ΙΐΒψCΉςCEΓΆCB”ΎΒψCΘ§”κMNΫΜ”ΎΒψEΘ§
ΓΏΓœACD=90ΓψΘ§
ΓύΓœACE=90ΓψΓœDCE,ΓœBCD=90ΓψΓœECDΘ§
ΓύΓœBCD=ΓœACE.
ÿDBâMNȧ
ΓύΓœCAE=90ΓψΓœAFC,ΓœD=90ΓψΓœBFDΘ§
ΓΏΓœAFC=ΓœBFDΘ§
ΓύΓœCAE=ΓœDΘ§
‘ΎΓςACEΚΆΓςDCB÷–, 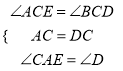 Θ§
Θ§
ΓύΓςACEΓ’ΓςDCB(ASA)Θ§
ΓύAE=DBΘ§CE=CBΘ§
ΓύΓςECBΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύBE=![]() CB.
CB.
”÷ΓΏBE=ABAEΘ§
ΓύBE=ABBDΘ§
ΓύABBD=![]() CB.
CB.
»γΆΦ(3):BDAB=![]() CB.άμ”…»γœ¬ΘΚ
CB.άμ”…»γœ¬ΘΚ
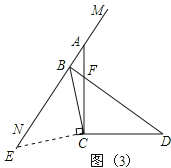
ΙΐΒψCΉςCEΓΆCB”ΎΒψCΘ§”κMNΫΜ”ΎΒψEΘ§
ΓΏΓœACD=90ΓψΘ§
ΓύΓœACE=90Γψ+ΓœACB,ΓœBCD=90Γψ+ΓœACBΘ§
ΓύΓœBCD=ΓœACE.
ÿDBâMNȧ
ΓύΓœCAE=90ΓψΓœAFB,ΓœD=90ΓψΓœCFDΘ§
ΓΏΓœAFB=ΓœCFDΘ§
ΓύΓœCAE=ΓœDΘ§
”÷ΓΏAC=DCΘ§
ΓύΓςACEΓ’ΓςDCBΘ§
ΓύAE=DBΘ§CE=CBΘ§
ΓύΓςECBΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύBE=![]() CB.
CB.
”÷ΓΏBE=AEAB,
ΓύBE=BDABΘ§
ΓύBDAB=![]() CB.
CB.
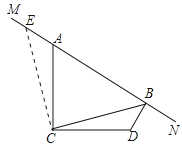
(3)MN‘Ύ»ΤΒψA–ΐΉΣΙΐ≥Χ÷–Θ§’βΗωΒΡ“βΥΦ≤ΔΟΜ”–÷ΗΟς «ΡΡ÷÷«ιΩωΘ§
ΓύΉέΚœΝΥΒΎ“ΜΗωΆΦΚΆΒΎΕΰΗωΆΦΝΫ÷÷«ιΩωΘ§
»τ «ΒΎ1ΗωΆΦΘΚ
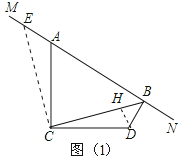
”…(1)ΒΟΘΚΓςACEΓ’ΓςDCBΘ§CE=CBΘ§
ΓύΓςECBΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύΓœAEC=45Γψ=ΓœCBDΘ§
ΙΐDΉςDHΓΆCB.‘ρΓςDHBΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΓΘ
BD=![]() BH,
BH,
ΓύBH=DH=1.
÷±Ϋ«ΓςCDH÷–,ΓœDCH=30ΓψΘ§
ΓύCD=2DH=2,CH=![]() .
.
ΓύCB=![]() +1ΘΜ
+1ΘΜ
»τ «ΒΎΕΰΗωΆΦΘΚΙΐDΉςDHΓΆCBΫΜCB―”≥ΛœΏ”ΎH.
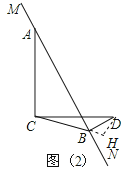
ΫβΖ®άύΥΤ…œΟφ,CD=2,ΒΟ≥ωCB=![]() 1ΘΜ
1ΘΜ
Ι ¥πΑΗΈΣΘΚ2, ![]() +1Μρ
+1Μρ![]() 1.
1.


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣA(-4Θ§2)ΓΔB(nΘ§-4) «“Μ¥ΈΚ· ΐ![]() ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐ
ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐ![]() ΒΡΆΦœσΒΡΝΫΗωΫΜΒψ.
ΒΡΆΦœσΒΡΝΫΗωΫΜΒψ.
Θ®1Θ©«σ¥ΥΖ¥±»άΐΚ· ΐΚΆ“Μ¥ΈΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©«σΓςAOBΒΡΟφΜΐΘΜ
Θ®3Θ©ΗυΨίΆΦœσ–¥≥ω Ι“Μ¥ΈΚ· ΐΒΡ÷Β–Γ”ΎΖ¥±»άΐΚ· ΐΒΡ÷ΒΒΡxΒΡ»Γ÷ΒΖΕΈß.
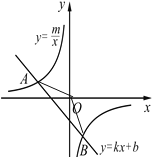
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒψPΘ®-5, 6Θ©”κΒψAΙΊ”Ύx÷αΕ‘≥ΤΘ§‘ρΒψAΒΡΉχ±ξΈΣ__________;
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷ΣA![]() Θ§B
Θ§B![]() Θ§C
Θ§C![]() »ΐΒψΘ§Τδ÷–aΓΔbΓΔc¬ζΉψΙΊœΒ Ϋ
»ΐΒψΘ§Τδ÷–aΓΔbΓΔc¬ζΉψΙΊœΒ Ϋ![]() Θ§
Θ§ ![]() .
.
(1) a= ΘΜb= ΘΜc= .
(2) »γΙϊ‘ΎΒΎΕΰœσœόΡΎ”–“ΜΒψP![]() Θ§«κ”ΟΚ§
Θ§«κ”ΟΚ§![]() ΒΡ ΫΉ”±μ ΨΥΡ±Ώ–ΈABOPΒΡΟφΜΐΘΜ
ΒΡ ΫΉ”±μ ΨΥΡ±Ώ–ΈABOPΒΡΟφΜΐΘΜ
(3) ‘Ύ(2)ΒΡΧθΦΰœ¬Θ§ «Ζώ¥φ‘ΎΒψPΘ§ ΙΥΡ±Ώ–ΈABOPΒΡΟφΜΐ”κΓςABCΒΡΟφΜΐœύΒ»ΘΩ»τ¥φ‘ΎΘ§«σ≥ωΒψPΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΓœAOB «÷±Ϋ«Θ§OEΤΫΖ÷ΓœAOCΘ§OFΤΫΖ÷ΓœBOCΘ° 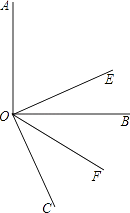
Θ®1Θ©»τΓœBOC=60ΓψΘ§«σΓœEOFΒΡΕ» ΐΘΜ
Θ®2Θ©»τΓœAOC=xΓψΘ®xΘΨ90Θ©Θ§¥Υ ±ΡήΖώ«σ≥ωΓœEOFΒΡ¥σ–ΓΘ§»τΡή«κ«σ≥ωΥϋΒΡ ΐ÷ΒΘΜ»τ≤ΜΡήΘ§«κ”ΟΚ§xΒΡ¥ζ ΐ Ϋά¥±μ ΨΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“Μ¥Έ ΐ―ß≤β―ι÷–Θ§Ρ≥–ΓΉιΈεΈΜΆ§―ßΒΡ≥…Φ®Ζ÷±π «ΘΚ110Θ§105Θ§90Θ§95Θ§90Θ§‘ρ’βΈεΗω ΐΨίΒΡ÷–ΈΜ ΐ «Θ®ΓΓΓΓΘ©
A.90
B.95
C.100
D.105
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥÷÷“©ΤΖ‘≠ά¥ έΦέ100‘ΣΘ§Ν§–χΝΫ¥ΈΫΒΦέΚσ έΦέΈΣ81‘ΣΘ§»τΟΩ¥Έœ¬ΫΒΒΡΑΌΖ÷¬ œύΆ§Θ§‘ρ’βΗωΑΌΖ÷¬ « Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΙϊa+6ΚΆ2a©¹15 «“ΜΗω ΐΒΡΤΫΖΫΗυΘ§‘ρ’βΗω ΐΈΣ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com