
【题目】已知二次函数![]() 的图象如图所示,对称轴为直线
的图象如图所示,对称轴为直线![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

A. ![]() B. 方程
B. 方程![]() 的两个根是
的两个根是![]() ,
,![]()
C. ![]() D. 当
D. 当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
【答案】B
【解析】
由抛物线开口得a>0,由抛物线与y轴的交点位置c<0,则可对A进行判断;由于抛物线的对称轴为直线x=1,则点(3,0)关于直线x=1的对称点为(1,0),于是得到抛物线与x轴交点坐标为(1,0)和(3,0),则可对B进行判断;根据抛物线的对称轴为直线x=![]() =1,则可对C进行判断;根据二次函数的性质可对D进行判断.
=1,则可对C进行判断;根据二次函数的性质可对D进行判断.
A、抛物线开口向上,则a>0,抛物线与y轴的交点在x轴下方,则c<0,所以ac<0,所以A选项错误;
B、抛物线的对称轴为直线x=1,点(3,0)关于直线x=1的对称点为(1,0),则方程ax2+bx+c=0的两个根是x1=1,x2=3,所以B选项正确;
C、抛物线的对称轴为直线x=![]() =1,则b=2a,即2a+b=0,所以C选项错误;
=1,则b=2a,即2a+b=0,所以C选项错误;
D、当0<x<1,y随x的增大而减小;x>1时,y随x的增大而增大,所以D选项错误.
故选:B.


科目:初中数学 来源: 题型:
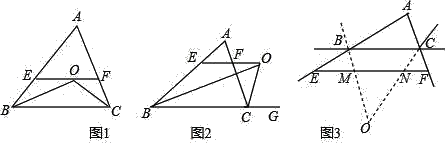
【题目】已知,如图1:△ABC中,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F
(1)直接写出图1中所有的等腰三角形.指出EF与BE、CF间有怎样的数量关系?
(2)在(1)的条件下,若AB=15,AC=10,求△AEF的周长;
(3)如图2,若△ABC中,∠B的平分线与三角形外角∠ACG的平分线CO交于点O,过O点作OE∥BC交AB于E,交AC于F,请问(1)中EF与BE、CF间的关系还是否存在,若存在,说明理由:若不存在,写出三者新的数量关系,并说明理由;
(4)如图3,∠ABC、∠ACB的外角平分线的延长线相交于点O,请直接写出EF,BE,CF,MN之间的数量关系.不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
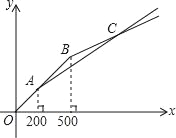
【题目】“五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.
(1)求在甲商店购物时y与x之间的函数关系;
(2)两种购物方式对应的函数图象如图所示,求交点C的坐标;
(3)根据图象,请直接写出“五一”期间选择哪家商店购物更优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边![]() 内一点
内一点![]() 将
将![]() 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() 已知
已知![]()
![]() .
.
![]() 求证:
求证:![]() 是等边三角形;
是等边三角形;
![]() 当
当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 探究:当
探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或解方程
(1)2![]() ﹣3
﹣3![]() +
+![]()
(2)(![]() ﹣2)(
﹣2)(![]() +2)﹣(
+2)﹣(![]() )2
)2
(3)(﹣3)0﹣![]() ﹣|1﹣
﹣|1﹣![]() |﹣
|﹣![]()
(4)3(3x﹣1)2﹣27=0
(5)![]() =﹣2
=﹣2
(6)![]() x﹣2=
x﹣2=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资![]() 万元用于该产品的广告促销,已知该产品的本地销售量
万元用于该产品的广告促销,已知该产品的本地销售量![]() (万台)与本地的广告费用
(万台)与本地的广告费用![]() (万元)之间的函数关系满足
(万元)之间的函数关系满足![]() .该产品的外地销售量
.该产品的外地销售量![]() (万台)与外地广告费用
(万台)与外地广告费用![]() (万元)之间的函数关系可用如图所示的抛物线和线段
(万元)之间的函数关系可用如图所示的抛物线和线段![]() 来表示.
来表示.
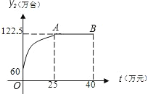
其中点![]() 为抛物线的顶点.
为抛物线的顶点.
![]() 结合图象,求出
结合图象,求出![]() (万台)与外地广告费用
(万台)与外地广告费用![]() (万元)之间的函数关系式;
(万元)之间的函数关系式;
![]() 求该产品的销售总量
求该产品的销售总量![]() (万台)与本地广告费用
(万台)与本地广告费用![]() (万元)之间的函数关系式;
(万元)之间的函数关系式;
![]() 如何安排广告费用才能使销售总量最大?
如何安排广告费用才能使销售总量最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=40°,分别以AB,AC为边作两个等腰三角形ABD和ACE,且AB=AD,AC=AE,∠BAD=∠CAE=90°.

(1)求∠DBC的度数.
(2)求证:BD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等边三角形.
(1)如图,点D在AB边上,点E在AC边上,BD=CE,BE与CD交于点F.试判断BF与CF的数量关系,并加以证明;
(2)点D是AB边上的一个动点,点E是AC边上的一个动点,且BD=CE,BE与CD交于点F.若△BFD是等腰三角形,求∠FBD的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com