
ЁОЬтФПЁПФГЙЋЫОПЊЗЂСЫвЛжжаТаЭЕФМвЕчВњЦЗЃЌгжЪЪЗъЁАМвЕчЯТЯчЁБЕФгХЛнеўВпЃЎЯжЭЖзЪ![]() ЭђдЊгУгкИУВњЦЗЕФЙуИцДйЯњЃЌвбжЊИУВњЦЗЕФБОЕиЯњЪлСП
ЭђдЊгУгкИУВњЦЗЕФЙуИцДйЯњЃЌвбжЊИУВњЦЗЕФБОЕиЯњЪлСП![]() ЃЈЭђЬЈЃЉгыБОЕиЕФЙуИцЗбгУ
ЃЈЭђЬЈЃЉгыБОЕиЕФЙуИцЗбгУ![]() ЃЈЭђдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕТњзу
ЃЈЭђдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕТњзу![]() ЃЎИУВњЦЗЕФЭтЕиЯњЪлСП
ЃЎИУВњЦЗЕФЭтЕиЯњЪлСП![]() ЃЈЭђЬЈЃЉгыЭтЕиЙуИцЗбгУ
ЃЈЭђЬЈЃЉгыЭтЕиЙуИцЗбгУ![]() ЃЈЭђдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕПЩгУШчЭМЫљЪОЕФХзЮяЯпКЭЯпЖЮ
ЃЈЭђдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕПЩгУШчЭМЫљЪОЕФХзЮяЯпКЭЯпЖЮ![]() РДБэЪОЃЎ
РДБэЪОЃЎ
ЦфжаЕу![]() ЮЊХзЮяЯпЕФЖЅЕуЃЎ
ЮЊХзЮяЯпЕФЖЅЕуЃЎ
![]() НсКЯЭМЯѓЃЌЧѓГі
НсКЯЭМЯѓЃЌЧѓГі![]() ЃЈЭђЬЈЃЉгыЭтЕиЙуИцЗбгУ
ЃЈЭђЬЈЃЉгыЭтЕиЙуИцЗбгУ![]() ЃЈЭђдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈЭђдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
![]() ЧѓИУВњЦЗЕФЯњЪлзмСП
ЧѓИУВњЦЗЕФЯњЪлзмСП![]() ЃЈЭђЬЈЃЉгыБОЕиЙуИцЗбгУ
ЃЈЭђЬЈЃЉгыБОЕиЙуИцЗбгУ![]() ЃЈЭђдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈЭђдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
![]() ШчКЮАВХХЙуИцЗбгУВХФмЪЙЯњЪлзмСПзюДѓЃП
ШчКЮАВХХЙуИцЗбгУВХФмЪЙЯњЪлзмСПзюДѓЃП
ЁОД№АИЁП![]() ЕБ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ![]() МћНтЮіЃЛ
МћНтЮіЃЛ![]() БОЕиЙуИцЗбгУЮЊ15ЭђдЊЃЌЭтЕиЙуИцЗбгУЮЊ25ЭђдЊ.
БОЕиЙуИцЗбгУЮЊ15ЭђдЊЃЌЭтЕиЙуИцЗбгУЮЊ25ЭђдЊ.
ЁОНтЮіЁП
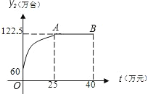
ЃЈ1ЃЉЗжЖЮЧѓНтЃЌЕБ0ЁмtЁм25ЪБЃЌвбжЊЖЅЕуAзјБъЃЌЩшЖЅЕуЪННтЮіЪНЃЌДњШывбжЊЕуЃЈ0,60ЃЉМДПЩЧѓНтЃЛЕБ25ЃМtЁм40ЪБЃЌy=122.5ЃЛ
ЃЈ2ЃЉгЩЬтвтПЩЕУt=40-xЃЌИљОнtЕФШЁжЕЗЖЮЇПЩШЗЖЈxЕФШЁжЕЗЖЮЇЮЊ0ЁмxЃМ15ЁЂ15ЁмxЃМ25ЁЂ25ЁмxЁм40ЃЌдђy=y1+y2ЃЌАДееxЕФЗЖЮЇЗжБ№ЧѓНт.
ЃЈ3ЃЉгЩЩЯЪіЫљЧѓБэДяЪНЗжБ№МЦЫуУПЖЮКЏЪ§ЕФзюДѓжЕЃЌдйШЁШ§ИіЪ§жЕжаЕФзюДѓжЕМДПЩ.
![]() гЩКЏЪ§ЭМЯѓПЩжЊЃЌ
гЩКЏЪ§ЭМЯѓПЩжЊЃЌ
ЕБ![]() ЪБЃЌКЏЪ§ЭМЯѓЮЊХзЮяЯпЕФвЛВПЗжЃЌ
ЪБЃЌКЏЪ§ЭМЯѓЮЊХзЮяЯпЕФвЛВПЗжЃЌ
ЩшНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
Аб![]() ДњШыНтЮіЪНЕУЃЌ
ДњШыНтЮіЪНЕУЃЌ
![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЛ
ЃЛ
![]() гЩЬтвтПЩЕУt=40-xЃЌИљОнtЕФШЁжЕЗЖЮЇЕУЃК
гЩЬтвтПЩЕУt=40-xЃЌИљОнtЕФШЁжЕЗЖЮЇЕУЃК
![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
![]() ЪБЃЌ
ЪБЃЌ![]()
![]() ЃЎ
ЃЎ
![]() ЪБЃЌзюДѓy=3ЁС15+122.5=167.5ЃЌ
ЪБЃЌзюДѓy=3ЁС15+122.5=167.5ЃЌ
![]() ЪБЃЌзюДѓy=-0.1ЁС625+122.5=60ЃЌ
ЪБЃЌзюДѓy=-0.1ЁС625+122.5=60ЃЌ
![]() ЪБЃЌзюДѓy=-0.1ЁС625+125=62.5ЃЌ
ЪБЃЌзюДѓy=-0.1ЁС625+125=62.5ЃЌ
ЙЪЕБx=15ЪБЃЌyжЕзюДѓЃЌ
ЙЪЃЌБОЕиЙуИцЗбгУЮЊ15ЭђдЊЃЌЭтЕиЙуИцЗбгУЮЊ25ЭђдЊ.


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
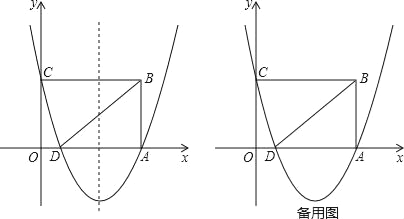
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЪЧдЕуЃЌОиаЮOABCЕФЖЅЕуAдкxжсЕФе§АыжсЩЯЃЌЖЅЕуCдкyЕФе§АыжсЩЯЃЌЕуBЕФзјБъЪЧЃЈ5ЃЌ3ЃЉЃЌХзЮяЯпy=![]() x2+bx+cОЙ§AЁЂCСНЕуЃЌгыxжсЕФСэвЛИіНЛЕуЪЧЕуDЃЌСЌНгBDЃЎ
x2+bx+cОЙ§AЁЂCСНЕуЃЌгыxжсЕФСэвЛИіНЛЕуЪЧЕуDЃЌСЌНгBDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуMЪЧХзЮяЯпЖдГЦжсЩЯЕФвЛЕуЃЌвдMЁЂBЁЂDЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§ЪЧ6ЃЌЧѓЕуMЕФзјБъЃЛ
ЃЈ3ЃЉЕуPДгЕуDГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиDЁњBдШЫйдЫЖЏЃЌЭЌЪБЕуQДгЕуBГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиBЁњAЁњDдШЫйдЫЖЏЃЌЕБЕуPЕНДяЕуBЪБЃЌPЁЂQЭЌЪБЭЃжЙдЫЖЏЃЌЩшдЫЖЏЕФЪБМфЮЊtУыЃЌЕБtЮЊКЮжЕЪБЃЌвдDЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃПЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
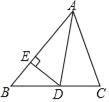
ЁОЬтФПЁПвбжЊЁїABCжаЃЌЁЯBЃН50ЁуЃЌЁЯCЃН70ЁуЃЌADЪЧЁїABCЕФНЧЦНЗжЯпЃЌDEЁЭABгкEЕуЃЎ
ЃЈ1ЃЉЧѓЁЯEDAЕФЖШЪ§ЃЛ
ЃЈ2ЃЉABЃН10ЃЌACЃН8ЃЌDEЃН3ЃЌЧѓSЁїABCЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃЌЖдГЦжсЮЊжБЯп
ЕФЭМЯѓШчЭМЫљЪОЃЌЖдГЦжсЮЊжБЯп![]() ЃЌдђЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
ЃЌдђЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ

A. ![]() B. ЗНГЬ
B. ЗНГЬ![]() ЕФСНИіИљЪЧ
ЕФСНИіИљЪЧ![]() ЃЌ
ЃЌ![]()
C. ![]() D. ЕБ
D. ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјдіДѓ
ЕФдіДѓЖјдіДѓ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЯпЖЮABКЭЩфЯпBMНЛгкЕуBЃЎ

ЃЈ1ЃЉРћгУГпЙцЭъГЩвдЯТзїЭМЃЌВЂБЃСєзїЭМКлМЃЃЈВЛаДзіЗЈЃЉ
ЂйдкЩфЯпBMЩЯзївЛЕуCЃЌЪЙACЃНABЃЌСЌНгAC
ЂкзїЁЯABMЕФНЧЦНЗжЯпНЛACгкЕуD
ЂлдкЩфЯпCMЩЯзївЛЕуEЃЌЪЙCEЃНCDЃЌСЌНгDE
ЃЈ2ЃЉдкЃЈ1ЃЉжаЫљзїЕФЭМаЮжаЃЌЭЈЙ§ЙлВьКЭВтСППЩвдЗЂЯжBDЃНDEЃЌЧыНЋЯТУцЕФжЄУїЙ§ГЬВЙГфЭъећжЄУїЃКЁпACЃНABЃЌ
ЁрЁЯЁЁ ЁЁЃНЁЯЁЁ ЁЁ
ЁпBDЦНЗжЁЯABMЃЌ
ЁрЁЯDBEЃНЉ![]() ЁЯЁЁ ЁЁ
ЁЯЁЁ ЁЁ
ЁпCEЃНCD
ЁрЁЯCDEЃНЁЯCED
ЁрЁЯACBЃНЁЯCDE+ЁЯCEDЃЌ
ЁрЁЯCEDЃН![]() ЁЯACB
ЁЯACB
ЁрЁЯDBEЃНЁЯCEDЃЌ
ЁрBDЃНDEЃЌЃЈЁЁ ЁЁЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌOCЦНЗжЁЯAOBЃЌЧвЁЯAOBЃН60ЁуЃЌЕуPЮЊOCЩЯШЮвтЕуЃЌPMЁЭOAгкMЃЌPDЁЮOAЃЌНЛOBгкDЃЌШєOMЃН3ЃЌдђPDЕФГЄЮЊ(ЁЁЁЁ)

A.2B.1.5C.3D.2.5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЁїABCЕФЮЛжУШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЗжБ№аДГіЁїABCИїИіЖЅЕуЕФзјБъЃЛ
ЃЈ2ЃЉХаЖЯЁїABCЕФаЮзДЃЛ
ЃЈ3ЃЉЧыдкЭМжаЛГіЁїABCЙигкyжсЖдГЦЕФЭМаЮЁїA'B'C'ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕЩЯгаЕуA(1ЃЌ0)ЃЌЕуAЕквЛДЮЬјЖЏжСЕуA1(Љ1ЃЌ1)ЃЌЕкЖўДЮЯђгвЬјЖЏ3ИіЕЅЮЛжСЕуA2(2ЃЌ1)ЃЌЕкШ§ДЮЬјЖЏжСЕуA3(Љ2ЃЌ2)ЃЌЕкЫФДЮЯђгвЬјЖЏ5ИіЕЅЮЛжСЕуA4(3ЃЌ2)ЃЌЁЃЌвдДЫЙцТЩЬјЖЏЯТШЅЃЌЕуAЕк2020ДЮЬјЖЏжСЕуA2020ЕФзјБъЪЧ( )

A.(1012ЃЌ1011)B.(1009ЃЌ1008)
C.(1010ЃЌ1009)D.(1011ЃЌ1010)
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com