
【题目】解方程:
![]()
![]()
![]()
![]() .
.
【答案】![]()
![]() ;(3)x1=
;(3)x1=![]() ,x2=
,x2=![]() ;(4)
;(4)![]() .
.
【解析】
(1)方程整理为一般形式,找出a,b,c的值,代入求根公式即可求出解.
(2)方程利用因式分解法求出解即可.
(3)利用开平方的定义解方程.
(4)方程移项,则左边是完全平方式,右边是常数,再利用直接开平方法即可求解.
(1)方程整理得:x2+2x﹣1=0,这里a=1,b=2,c=﹣1.
∵△=4+4=8,∴x=![]() ,∴x1=
,∴x1=![]() ,x2=
,x2=![]() ;
;
(2)分解因式得:(x﹣3)(x﹣3+2)=0,可得x﹣3=0或x﹣1=0,解得:x1=3,x2=1.
(3)移项得:(x﹣2)2=27
开平方得:x﹣2=±3![]()
移项得:x1=![]() ,x2=
,x2=![]() .
.
(4)∵3x2+1=2![]() x,∴3x2﹣2
x,∴3x2﹣2![]() x+1=0,∴(
x+1=0,∴(![]() x﹣1)2=0,∴x1=x2=
x﹣1)2=0,∴x1=x2=![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=﹣x2+bx+c的图象如图所示,下列几个结论:
①对称轴为x=2;②当y≤0时,x<0或x>4;③函数解析式为y=﹣x(x+4);④当x≤0时,y随x的增大而增大.其中正确的结论有_____
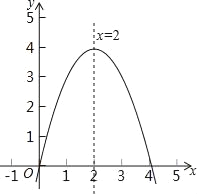
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边![]() 内一点
内一点![]() 将
将![]() 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() 已知
已知![]()
![]() .
.
![]() 求证:
求证:![]() 是等边三角形;
是等边三角形;
![]() 当
当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 探究:当
探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,错误的是( )
A. 二次函数![]() 的图象是开口向上的抛物线
的图象是开口向上的抛物线
B. 二次函数![]() 的图象必在
的图象必在![]() 轴上方
轴上方
C. 二次函数图象的对称轴是![]() 轴或与
轴或与![]() 轴平行的直线
轴平行的直线
D. 二次函数图象的顶点必在图象的对称轴上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资![]() 万元用于该产品的广告促销,已知该产品的本地销售量
万元用于该产品的广告促销,已知该产品的本地销售量![]() (万台)与本地的广告费用
(万台)与本地的广告费用![]() (万元)之间的函数关系满足
(万元)之间的函数关系满足![]() .该产品的外地销售量
.该产品的外地销售量![]() (万台)与外地广告费用
(万台)与外地广告费用![]() (万元)之间的函数关系可用如图所示的抛物线和线段
(万元)之间的函数关系可用如图所示的抛物线和线段![]() 来表示.
来表示.
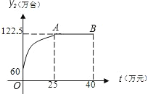
其中点![]() 为抛物线的顶点.
为抛物线的顶点.
![]() 结合图象,求出
结合图象,求出![]() (万台)与外地广告费用
(万台)与外地广告费用![]() (万元)之间的函数关系式;
(万元)之间的函数关系式;
![]() 求该产品的销售总量
求该产品的销售总量![]() (万台)与本地广告费用
(万台)与本地广告费用![]() (万元)之间的函数关系式;
(万元)之间的函数关系式;
![]() 如何安排广告费用才能使销售总量最大?
如何安排广告费用才能使销售总量最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,边长为a、b的矩形,它的周长为14,面积为10,求a2b+3a3b3+ab2的值;

(2)已知a+b=8,ab=16+c2,求(a﹣b+c)2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在北部湾经济区农业示范基地采购A,B两种农产品,已知A种农产品每千克的进价比B种多2元,且用24000元购买A种农产品的数量(按重量计)与用18000元购买B种农产品的数量(按重量计)相同.
(1)求A,B两种农产品每千克的进价分别是多少元?
(2)该公司计划购进A,B两种农产品共40吨,并运往异地销售,运费为500元/吨,已知A种农产品售价为15元/kg,B种农产品售价为12元/kg,其中A种农产品至少购进15吨且不超过B种农产品的数量,问该公司应如何采购才能获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com