
【题目】如图,OC平分∠AOB,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=3,则PD的长为( )

A.2B.1.5C.3D.2.5
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(0,3),B(![]() ,0),AB =6,作∠DBO=∠ABO,点H为y轴上的点,∠CAH=∠BAO,BD交y轴于点E,直线DO交AC于点C.
,0),AB =6,作∠DBO=∠ABO,点H为y轴上的点,∠CAH=∠BAO,BD交y轴于点E,直线DO交AC于点C.
(1)证明:△ABE为等边三角形;
(2)若CD⊥AB于点F,求线段CD的长;
(3)动点P从A出发,沿A﹣O﹣B路线运动,速度为1个单位长度每秒,到B点处停止运动;动点Q从B出发,沿B﹣O﹣A路线运动,速度为2个单位长度每秒,到A点处停止运动.两点同时开始运动,都要到达相应的终点才能停止.在某时刻,作PM⊥CD于点M,QN⊥CD于点N.问两动点运动多长时间时△OPM与△OQN全等?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边![]() 内一点
内一点![]() 将
将![]() 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() 已知
已知![]()
![]() .
.
![]() 求证:
求证:![]() 是等边三角形;
是等边三角形;
![]() 当
当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 探究:当
探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资![]() 万元用于该产品的广告促销,已知该产品的本地销售量
万元用于该产品的广告促销,已知该产品的本地销售量![]() (万台)与本地的广告费用
(万台)与本地的广告费用![]() (万元)之间的函数关系满足
(万元)之间的函数关系满足![]() .该产品的外地销售量
.该产品的外地销售量![]() (万台)与外地广告费用
(万台)与外地广告费用![]() (万元)之间的函数关系可用如图所示的抛物线和线段
(万元)之间的函数关系可用如图所示的抛物线和线段![]() 来表示.
来表示.
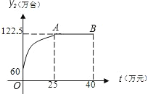
其中点![]() 为抛物线的顶点.
为抛物线的顶点.
![]() 结合图象,求出
结合图象,求出![]() (万台)与外地广告费用
(万台)与外地广告费用![]() (万元)之间的函数关系式;
(万元)之间的函数关系式;
![]() 求该产品的销售总量
求该产品的销售总量![]() (万台)与本地广告费用
(万台)与本地广告费用![]() (万元)之间的函数关系式;
(万元)之间的函数关系式;
![]() 如何安排广告费用才能使销售总量最大?
如何安排广告费用才能使销售总量最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,边长为a、b的矩形,它的周长为14,面积为10,求a2b+3a3b3+ab2的值;

(2)已知a+b=8,ab=16+c2,求(a﹣b+c)2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=40°,分别以AB,AC为边作两个等腰三角形ABD和ACE,且AB=AD,AC=AE,∠BAD=∠CAE=90°.

(1)求∠DBC的度数.
(2)求证:BD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在北部湾经济区农业示范基地采购A,B两种农产品,已知A种农产品每千克的进价比B种多2元,且用24000元购买A种农产品的数量(按重量计)与用18000元购买B种农产品的数量(按重量计)相同.
(1)求A,B两种农产品每千克的进价分别是多少元?
(2)该公司计划购进A,B两种农产品共40吨,并运往异地销售,运费为500元/吨,已知A种农产品售价为15元/kg,B种农产品售价为12元/kg,其中A种农产品至少购进15吨且不超过B种农产品的数量,问该公司应如何采购才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④ AE2+DF2=AF2+DE2.上述结论中正确的是( )
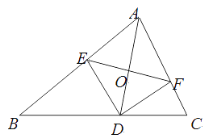
A. ②③ B. ②④ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2﹣(2m﹣1)x+m2+1=0.
(1)若方程有实数根,求实数m的取值范围;
(2)设x1,x2分别是方程的两个根,且满足x12+x22=x1x2+10,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com