
【题目】如图,在平面直角坐标系中,点A(0,3),B(![]() ,0),AB =6,作∠DBO=∠ABO,点H为y轴上的点,∠CAH=∠BAO,BD交y轴于点E,直线DO交AC于点C.
,0),AB =6,作∠DBO=∠ABO,点H为y轴上的点,∠CAH=∠BAO,BD交y轴于点E,直线DO交AC于点C.
(1)证明:△ABE为等边三角形;
(2)若CD⊥AB于点F,求线段CD的长;
(3)动点P从A出发,沿A﹣O﹣B路线运动,速度为1个单位长度每秒,到B点处停止运动;动点Q从B出发,沿B﹣O﹣A路线运动,速度为2个单位长度每秒,到A点处停止运动.两点同时开始运动,都要到达相应的终点才能停止.在某时刻,作PM⊥CD于点M,QN⊥CD于点N.问两动点运动多长时间时△OPM与△OQN全等?


【答案】(1)详见解析;(2)CD=![]() ;(3)当两动点运动时间为
;(3)当两动点运动时间为![]() 、
、![]() 、6秒时,△OPM与△OQN全等.
、6秒时,△OPM与△OQN全等.
【解析】
(1)先证△AOB≌△EOB得到AE=BE=AB,从而可以得出结论;
(2)由(1)知∠ABE=∠BEA=∠EAB=60°,进而得出∠AOF=30°,利用含30°角的直角三角形的性质得到AF、OF的长.再证明∠ACF=∠AOF=30°,∠D=30°,同理得出CF、DF的长,进而可得出结论.
(3)设运动的时间为t秒.然后分四种情况讨论:①当点P、Q分别在y轴、x轴上时,![]() ;②当点P、Q都在y轴上时,
;②当点P、Q都在y轴上时,![]() ;③当点P在x轴上,Q在y轴且二者都没有提前停止时,
;③当点P在x轴上,Q在y轴且二者都没有提前停止时,![]() ;④当点P在x轴上,Q在y轴且点Q提前停止时,
;④当点P在x轴上,Q在y轴且点Q提前停止时,![]() ,列方程求解即可.
,列方程求解即可.
(1)在△AOB与△EOB中,∵∠AOB=∠EOB,OB=OB,∠EBO=∠ABO,∴△AOB≌△EOB (ASA),∴AO=EO=3,BE=AB=6,∴AE=BE=AB=6,∴△ABE为等边三角形.
(2)由(1)知∠ABE=∠BEA=∠EAB=60°.
∵CD⊥AB,∴∠AOF=30°,∴AF=![]() .
.
在Rt△AOF中,OF=![]() .
.
∵∠CAH=∠BAO =60°,∴∠CAF =60°,∠ACF=∠AOF=30°,∴AO=AC.
又∵CD⊥AB,∴CF=![]() .
.
∵AB=6,AF=![]() ,∴BF=
,∴BF=![]() .
.
在Rt△BDF中,∠DBF =60°,∠D=30°,∴BD=![]() .
.
由勾股定理得:∴DF=![]() ,∴CD=
,∴CD=![]() .
.
(3)设运动的时间为t秒.
①当点P、Q分别在y轴、x轴上时,![]() ,PO=QO得:
,PO=QO得:![]() ,解得:
,解得:![]() (秒);
(秒);
②当点P、Q都在y轴上时,![]() ,PO=QO得:
,PO=QO得:![]() ,解得
,解得![]() (秒);
(秒);
③当点P在x轴上,Q在y轴且二者都没有提前停止时,![]() ,则PO=QO,得:
,则PO=QO,得:![]() ,解得:
,解得:![]() ,不合题意,舍去.
,不合题意,舍去.
④当点P在x轴上,Q在y轴且点Q提前停止时,![]() 有
有![]() ,解得:
,解得:![]() (秒).
(秒).
综上所述:当两动点运动时间为![]() 、
、![]() 、6秒时,△OPM与△OQN全等.
、6秒时,△OPM与△OQN全等.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将一个等腰直角三角形按图中方式依次翻折,若DE=a,DC=b,则下列说法:①DC′平分∠BDE;②BC的长为2a+b;③△BC′D是等腰三角形;④△CED的周长等于BC的长.其中正确的是()

A.①②③B.②④C.②③④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
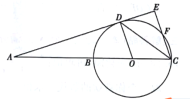
【题目】如图,点D是⊙O上一点,直线AE经过点D,直线AB经过圆心O,交⊙O于B,C两点,CE⊥AE,垂足为点E,交⊙O于点F,∠BCD=∠DCF
(1)求∠A+∠BOD的度数;
(2)若sin∠DCE=![]() ,⊙O的半径为5,求线段AB的长.
,⊙O的半径为5,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
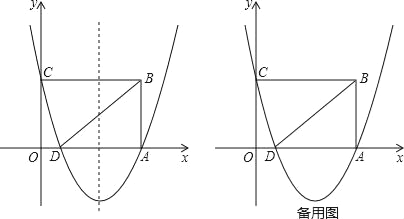
【题目】如图,在平面直角坐标系中,点O是原点,矩形OABC的顶点A在x轴的正半轴上,顶点C在y的正半轴上,点B的坐标是(5,3),抛物线y=![]() x2+bx+c经过A、C两点,与x轴的另一个交点是点D,连接BD.
x2+bx+c经过A、C两点,与x轴的另一个交点是点D,连接BD.
(1)求抛物线的解析式;
(2)点M是抛物线对称轴上的一点,以M、B、D为顶点的三角形的面积是6,求点M的坐标;
(3)点P从点D出发,以每秒1个单位长度的速度沿D→B匀速运动,同时点Q从点B出发,以每秒1个单位长度的速度沿B→A→D匀速运动,当点P到达点B时,P、Q同时停止运动,设运动的时间为t秒,当t为何值时,以D、P、Q为顶点的三角形是等腰三角形?请直接写出所有符合条件的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=45°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )

A. ①②④ B. ②③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠ACB=90°,AC=8,BC=6,点E是AB中点,将△CAE沿着直线CE翻折,得到△CDE,连接AD,则点E到线段AD的距离等于( )

A.2B.1.8C.1.5D.1.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,已知AB∥CD,AD⊥AB,AD=2,AB+CD=4,点E为BC的中点.

(1)求四边形ABCD的面积;
(2)若AE⊥BC,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
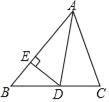
【题目】已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC平分∠AOB,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=3,则PD的长为( )

A.2B.1.5C.3D.2.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com