如图，已知线段 AB 和 CD 的公共部分为 BD，且 BD=
AB= 
CD，线段 AB、CD 的中点 E、F
之间距离是 20，求 AB、CD 的长．
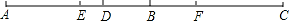
【考点】两点间的距离．
【分析】根据线段中点的性质，可得 AE=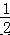
AB，CF= 
CD，根据线段的和差，可得 AC 的长、EF 的 长，根据解方程，可得 x 的值．
【解答】解：设 BD=x，则 AB=3x，CD=4x．
∵点 E、点 F 分别为 AB、CD 的中点，
∴AE= 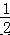AB=1.5x，CF= 
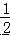CD=2x，
AC=AB+CD﹣BD=3x+4x﹣x=6x．
∴EF=AC﹣AE﹣CF=6x﹣1.5x﹣2x=2.5x．
∵EF=20，
∴2.5x=20， 解得：x=8．
∴AB=3x=24，CD=4x=32．
【点评】本题考查了两点间的距离，利用 BD=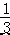
AB=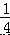 
CD 得出 BD=x，则 AB=3x，CD=4x，AC=6x
是解题关键．
阅读快车系列答案科目：初中数学 来源： 题型：
为了节约用水，某市规定三口之家每月标准用水量为 15 立方米，超过部分加价收费，假设不超
过部分水费为 1.5 元/立方米，超过部分水费为 3 元/立方米．
（1）当每月用水量为 a 立方米时，请用代数式分别表示这家按标准用水量和超出标准用水时各应缴 纳的水费；
如果甲、乙两家用水量分别为 10 立方米和 20 立方米，那么甲、乙两家该月应各交多少水费？
（3）当丁家本月交水费 46.5 元时，那么丁家该月用水多少立方米？
查看答案和解析>>
科目：初中数学 来源： 题型：
某超市规定，如果购买不超过 50 元的商品时，按全额收费；购买超过 50 元的商品时，超过部
分按九折收费．某顾客在一次消费中，向售货员交纳了 212 元，那么在此次消费中该顾客购买了价 值 元的商品．
查看答案和解析>>
科目：初中数学 来源： 题型：
某校为了满足学生借阅图书的需求，计划购买一批新书．为此，该校图书管理员对一周内本校 学生从图书馆借出各类图书的数量进行了统计．结果如图：
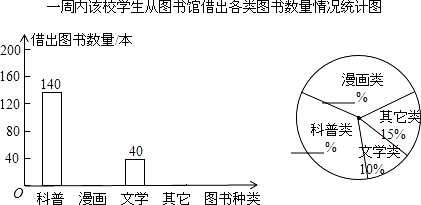
请你根据统计图中的信息，解答下列问题：
（1）补全条形统计图和扇形统计图； 该校学生最喜欢借阅哪类图书？
（3）该校计划购买新书共 600 本，若按扇形统计图中的百分比来相应的确定漫画、科普、文学、其 它这四类图书的购买量，求应购买这四类图书各多少本？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
[2﹣（﹣3）2 ．
无解，则 k 的值为