
【题目】某批足球的质量检测结果如下:
抽取足球数n | 100 | 200 | 400 | 600 | 800 | 1000 |
合格的频数m | 93 | 192 | 384 | 564 | 759 | 950 |
合格的频率 | 0.93 | 0.96 | 0.96 | 0.94 |
(1)填写表中的空格;(结果保留0.01)
(2)画出合格的频率的折线统计图;
(3)从这批足球任意抽取的一只足球是合格品的概率是多少?并说明理由.

【答案】(1)详见解析;(2)详见解析;(3)0.95
【解析】
(1)根据频率=频数÷总数计算可得;
(2)由表格中数据在坐标系内用点描出来,再用线段依次相连即可得;
(3)根据频率估计概率,频率都在0.95左右波动,所以任意抽取的一只足球是合格品的概率估计值是0.95.
解:(1)759÷800=0.95,
950÷1000=0.95.
完成表格如下:
抽取足球数n | 100 | 200 | 400 | 600 | 800 | 1000 |
合格的频数m | 93 | 192 | 384 | 564 | 759 | 950 |
合格的频率 | 0.93 | 0.96 | 0.96 | 0.94 | 0.95 | 0.95 |
(2)如图所示:
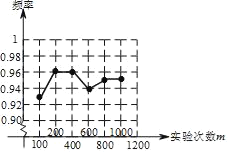
(3)从这批足球任意抽取的一只足球是合格品的概率估计值0.95,
因为从折线统计图中可知,随着实验次数的增大,频率逐渐稳定到常数0.95附近,
所以从这批足球任意抽取的一只足球是合格品的概率估计值0.95.


科目:初中数学 来源: 题型:
【题目】某文具店A类笔的标价是B类笔标价的1.2倍,某顾客用240元买笔,能单独购买A笔的数量恰好比单独购买B类笔的数量少4支.
(1)求A,B两类笔的标价;
(2)若A类笔的进价为8元/支,B类笔的进价为7元/支.文具店老板准备用不超过760元购进两类笔共100支,应如何进货才能获得最大利润?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE是□ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E、连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF:BE=2:3;④S四边形AFOE:S△COD=2:3.其中正确的结论有( )个.
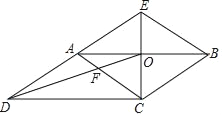
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD⊥弦AB于点C,连接BO并延长交⊙O于点E,连接AE,若AB=6,CD=1,则AE的长为( )
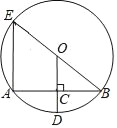
A. 3![]() B. 8 C. 12 D. 8
B. 8 C. 12 D. 8![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2017年3月起,成都市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第I级:居民每户每月用水18吨以内含18吨每吨收水费a元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过部分每吨收水费b元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第I、Ⅱ级标准收费,超过部分每吨收水费c元.
设一户居民月用水x吨,应缴水费为y元,y与x之间的函数关系如图所示
(1)根据图象直接作答:a= ,b= ;
(2)求当x≥25时y与x之间的函数关系;
(3)把上述水费阶梯收费办法称为方案①,假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费,请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.(写出过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=![]() (x>0)的图象经过A,B两点.若点A的坐标为(n,1),则 k的值为______.
(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则 k的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.

(1)求证:AE平分∠DAC;
(2)若AB=6,∠ABE=60°.
①求AD的长; ②求出图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com