
 如图,一张长方形桌子的桌面长100cm,宽60cm,一块长方形台布的面积是桌面面积是2$\frac{3}{4}$倍,并且铺在桌面上时,各边垂下的长度相等,求台布的长和宽.
如图,一张长方形桌子的桌面长100cm,宽60cm,一块长方形台布的面积是桌面面积是2$\frac{3}{4}$倍,并且铺在桌面上时,各边垂下的长度相等,求台布的长和宽. 分析 设台布下垂长度为x,则台布面积为(100+2x)(60+2x)m2,运用台布面积是桌面面积的2$\frac{3}{4}$倍可列出一元二次方程,求解即可得出答案.
解答 解:设台布下垂长度为x,则台布面积为(100+2x)(60+2x)m2,
得方程(100+2x)(60+2x)=2$\frac{3}{4}$×100×60,
解得x1=-97(舍去),x2=33,
则台布长为100+2x=100+2×33=166(cm),
宽为60+2x=60+2×33=126(cm).
答:这块台布的长为166cm,宽120cm.
点评 此题考查一元二次方程的应用,解答本题的关键是表示出台布的面积,利用台布面积是桌面面积的2倍建立方程,难度一般,注意细心求解.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$的解集是x<-1.
如图所示,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$的解集是x<-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的负半轴上,点C在y轴的正半轴上,OA=5,OC=4,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的负半轴上,点C在y轴的正半轴上,OA=5,OC=4,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,BC=8cm,AG∥BC,AG=8cm,点F从点B出发,沿线段BC以4cm/s的速度连续做往返运动,点E从点A出发沿线段AG以2cm/s的速度运动至点G.E、F两点同时出发,当点E到达点G时,E、F两点同时停止运动,EF与AC交于点D,设点E的运动时间为t(秒).
如图,在△ABC中,BC=8cm,AG∥BC,AG=8cm,点F从点B出发,沿线段BC以4cm/s的速度连续做往返运动,点E从点A出发沿线段AG以2cm/s的速度运动至点G.E、F两点同时出发,当点E到达点G时,E、F两点同时停止运动,EF与AC交于点D,设点E的运动时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
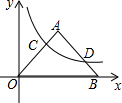 如图,双曲线y=$\frac{k}{x}$在第一象限内的图象与等腰直角三角形OAB相交于C点和D点,∠A=90°,OA=1,OC=2BD,则k的值是$\frac{8}{25}$.
如图,双曲线y=$\frac{k}{x}$在第一象限内的图象与等腰直角三角形OAB相交于C点和D点,∠A=90°,OA=1,OC=2BD,则k的值是$\frac{8}{25}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com