
如图,抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0)、B(3,0)、C(0,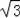
 )三点.
)三点.
(1)求抛物线的函数表达式;
(2)求证:点C在以AB为直径的圆上;
(3)以BC为直径作⊙P,点D为抛物线上一动点,是否存在点D使直线OD与⊙P相切?若存在,请求出点D的坐标;若不存在,请说明理由.


【考点】二次函数综合题.
【分析】(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;
(2)由条件可求得AC、BC、AB,可证明△ABC为直角三角形,可证得结论;
(3)由条件可先求得P点坐标,连接OD,由切线的性质可得到∠POB=∠AOD,过P作PE⊥AB于点E,过D作DF⊥AB于点F,设出D点坐标,根据tan∠BOP=tan∠ODF,再结合D点在抛物线上,可求得D点坐标.
【解答】(1)解:∵抛物线经过A(﹣1,0)、B(3,0)、C(0,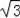
 )三点,
)三点,
∴把三点坐标代入可得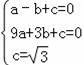
 ,
,
解得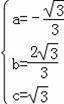
 .
.
∴抛物线解析式为y=﹣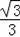
 x2+
x2+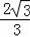
 x+
x+
 ;
;
(2)证明:∵A(﹣1,0)、B(3,0)、C(0,
 ),
),
∴OA=1,BO=3,OC=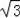
 ,
,
∴AB=4,
在Rt△AOB中,可求得AC=2,在Rt△BOC中可求得BC=2
 ,
,
∴AC2+BC2=4+12=16=AB2,
∴∠ACB=90°,
∵AB为直径,
∴点C在以AB为直径的圆上;
(3)解:存在.理由如下:
∵B(3,0),C(0,
 )
)
∴P(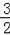
 ,
,
 ),
),
设直线OP解析式为y=kx,代入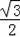
 =
=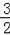
 k,解k=
k,解k=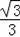
 ,
,
∴直线OP的y=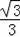
 x,
x,
∴OD为⊙P的切线,
∴OD⊥OP,
∴直线OD的解析式为y=﹣
 x,
x,
联立直线OD和抛物线解析式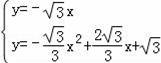
 ,解得
,解得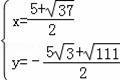
 或
或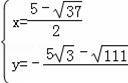
 ,
,
∴D点坐标为(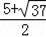
 ,
,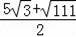
 )或(
)或(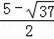
 ,
,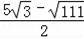
 ),
),
综上可知存在满足条件的D点,其坐标为(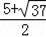
 ,
,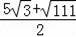
 )或(
)或(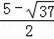
 ,
,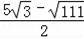
 ).
).
【点评】本题主要考查二次函数的综合应用,涉及待定系数法、勾股定理及其逆定理、圆周角定理、切线的性质等知识点.在(1)中注意待定系数法的步骤,在(2)中证得∠ACB为直角是解题的关键,在(3)中求得直线OD的解析式是解题的关键.本题考查知识点较多,综合性较强,难度较大.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
某篮球队12名队员的年龄如表:
| 年龄(岁) | 18 | 19 | 20 | 21 |
| 人数 | 5 | 4 | 1 | 2 |
则这12名队员年龄的众数和平均数分别是( )
A.18,19 B.19,19 C.18,19.5 D.19,19.5
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的一元二次方程(a+c)x2-2bx+(a-c)=0,其中a,b,c分 别为△ABC三
别为△ABC三
边长.
(1)若方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(2)若△ABC是等 边三角形,试求这个一元二次方程的根.
边三角形,试求这个一元二次方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
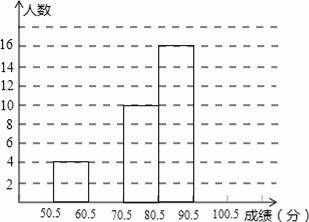
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有850名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成并有局部污染的频率分布表和频率分布直方图,解答下列问题:
| 分 组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 |
| 0.16 |
| 70.5~80.5 | 10 |
|
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 |
|
|
| 合 计 | 50 | 1.00 |
(1)填充频率分布表的空格;
(2)补全频数直方图,并在此图上直接绘制频数分布折线图;
(3)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC的度数为x,,请直接写出∠DOE的度数(用含有x的式子表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转到图②的位置,试探究∠AOC与∠DOE的度数之间的关系,
写出你的结论,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com