
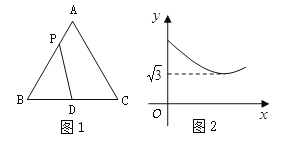
【题目】如图1,在等边△ABC中,点D是BC边的中点,点P为AB 边上的一个动点,设AP= ![]() ,PD=
,PD= ![]() ,若
,若![]() 与
与![]() 之间的函数关系的图象如图2所示,则等边△ABC的面积为( )
之间的函数关系的图象如图2所示,则等边△ABC的面积为( )
A. 4 B. ![]() C. 12 D.
C. 12 D. ![]()
【答案】D
【解析】从图2的函数图象为抛物线得知,y与x满足二次函数关系,同时y的最小值为![]() ,结合等边三角形的图形可知,当点P运动到DP⊥AD位置时,DP长为最小值,利用等边三角形的特殊角可求出边长,从而得出等边三角形ABC的面积.
,结合等边三角形的图形可知,当点P运动到DP⊥AD位置时,DP长为最小值,利用等边三角形的特殊角可求出边长,从而得出等边三角形ABC的面积.
解:由图二可得y最小值=![]() ,
,
∵△ABC为等边三角形,分析图一可知,当P点运动到DP⊥AB时,DP长为最小值,
∴此时的DP=![]() ,
,
∵∠B=60°,
∴sin60°=![]() ,解得BD=2,
,解得BD=2,
∵D为BC的中点,
∴BC=4,连接AD,
∵△ABC为等边三角形,
∴AD⊥BC,
∴sin60°=![]() ,
,
∴AD=2![]() ,∴S△ABC=
,∴S△ABC=![]() ×4×2
×4×2![]() =4
=4![]() .
.
故选D.
“点睛”本题通过函数图象把动点带来的最小值进行了呈现,正确理解P点运动到何处时DP长最小是关键,同时也考查了3对函数的观察,难度适中.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
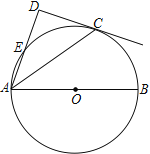
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O 于点E.
(1) 求证:AC平分∠DAB;
(2) 连接CE,若CE=6,AC=8,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设点A(﹣1,y1)、B(1,y2)、C(2,y3)是抛物线y=﹣2(x﹣1)2+m上的三点,则y1、y2,y3的大小关系的是_____(用“<”连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3, ![]() ),点C的坐标为(
),点C的坐标为( ![]() ,0),点P为斜边OB上的一动点,则PA+PC的最小值为
,0),点P为斜边OB上的一动点,则PA+PC的最小值为 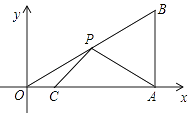
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ. 
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①对角线互相平分且垂直的四边形是菱形;
②一组对边平行,一组对边相等的四边形是平行四边形;
③有一个角是直角的四边形是矩形;
④对角线相等且垂直的四边形是正方形
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是( ) 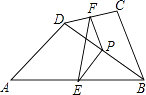
A.15°
B.20°
C.25°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解外来务工子女就学情况,某校对七年级各班级外来务工子女的人数情况进行了统计,发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅统计图:
(1)求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整;
(2)学校决定从只有2名外来务工子女的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名外来务工子女来自同一个班级的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com