
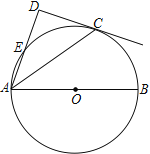
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O 于点E.
(1) 求证:AC平分∠DAB;
(2) 连接CE,若CE=6,AC=8,求AE的长.
【答案】(1)证明见解析;(2)2.8.
【解析】试题分析:(1)连接OC,利用条件可证得AD∥OC,再根据平行线的性质和角之间的关系可得∠DAC=∠CAO,即可得证;
(2)连接BC、OE,根据圆周角定理和勾股定理可求AB的长,然后根据相似三角形的判定和性质可得到AD=4.8,DE=3.6,由此可解.
试题解析:(1)证明:连接OC,则OC⊥CD,又AD⊥CD,∴∠ADC=∠OCD=90°,
∴AD∥OC,∴∠CAD=∠OCA,
又OA=OC,∴∠OCA=∠OAC,
∴∠CAD=∠CAO,∴AC平分∠DAB.
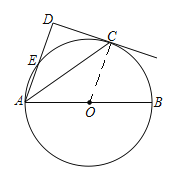
(2)解:连接BC、OE,
∵∠EOA=2∠CAD,∠COB=2∠CAO
∵∠CAD=∠CAO,∴∠EOA=∠COB
∴BC=EC=6
∵AB是⊙O的直径,∴∠ACB=90°,
又AC=8,勾股定理易得AB=10,
∵∠DAC=∠CAB,∠ADC=∠ACB=90°,
∴△ADC∽△ACB,∴![]() ,
,
∴AD=![]() =6.4,
=6.4,
又∠DEC=∠ABC,同理可得DE=3.6,
∴AE=AD-DE=6.4-3.6=2.8.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F. 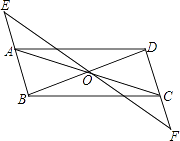
(1)求证:△AOE≌△COF;
(2)请连接EC、AF,则EF与AC满足什么条件时,四边形AECF是矩形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资量
与投资量![]() 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润![]() 与投资量
与投资量![]() 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)

(1)分别求出利润![]() 与
与![]() 关于投资量
关于投资量![]() 的函数关系式;
的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:

(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
科目:初中数学 来源: 题型:
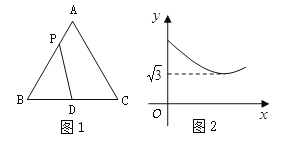
【题目】如图1,在等边△ABC中,点D是BC边的中点,点P为AB 边上的一个动点,设AP= ![]() ,PD=
,PD= ![]() ,若
,若![]() 与
与![]() 之间的函数关系的图象如图2所示,则等边△ABC的面积为( )
之间的函数关系的图象如图2所示,则等边△ABC的面积为( )
A. 4 B. ![]() C. 12 D.
C. 12 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE. 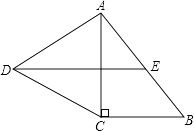
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com