
如图,在平面直角坐标系xOy中,⊙A与y轴相切于点 ,与x轴相交于M、N两点.如果点M的坐标为
,与x轴相交于M、N两点.如果点M的坐标为 ,求点N的坐标.
,求点N的坐标.

【考点】切线的性质;坐标与图形性质;勾股定理;垂径定理.
【分析】连接AB、AM、过A作AC⊥MN于C,设⊙A的半径是R,根据切线性质得出AB=AM=R,求出CM=R﹣ ,AC=
,AC=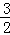 ,MN=2CM,
,MN=2CM,
由勾股定理得出方程R2=(R﹣ )2+(
)2+(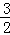 )2,求出方程的解即可.
)2,求出方程的解即可.
【解答】解: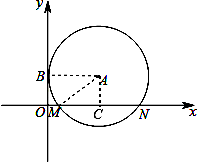
连接AB、AM、过A作AC⊥MN于C,设⊙A的半径是R,
∵⊙A与y轴相切于B,
∴AB⊥y轴,
∵点 ,与x轴相交于M、N两点,点M的坐标为
,与x轴相交于M、N两点,点M的坐标为 ,
,
∴AB=AM=R,CM=R﹣ ,AC=
,AC=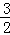 ,MN=2CM,
,MN=2CM,
由勾股定理得:R2=(R﹣ )2+(
)2+(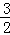 )2,
)2,
R=2.5,
∴CM=CN=2.5﹣ =2,
=2,
∴ON= +2+2=4
+2+2=4 ,
,
即N的坐标是(4 ,0).
,0).
【点评】本题考查了切线的性质,勾股定理,垂径定理的应用,关键是能根据题意得出关于R的方程.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
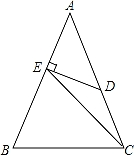
已知:如图,在△ABC中,AB=AC,∠A=45°,点D在AC上,DE⊥AB于E,且DE=DC,连结EC.请写出图中所有 等腰三角形(△ABC除外),并说明理由.
等腰三角形(△ABC除外),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
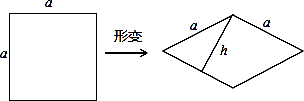
如图,边长为a的正方形发生形变后成为边长为a的菱形,如果这个菱形的一组对边之间的距离为h,记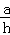 =k,我们把k叫做这个菱形的“形变度”.若变形后的菱形有一个角是60°,则形变度k= .
=k,我们把k叫做这个菱形的“形变度”.若变形后的菱形有一个角是60°,则形变度k= .
查看答案和解析>>
科目:初中数学 来源: 题型:
如果三角形有一个边上的中线长恰好等于这个边的长,那么称这个三角形是“有趣三角形”,这条中线为“有趣中线”.如图,在△ABC中,∠C=90°,较短的一条直角边BC=1,且△ABC是“有趣三角形”,求△ABC的“有趣中线”的长.
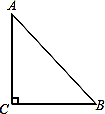
查看答案和解析>>
科目:初中数学 来源: 题型:
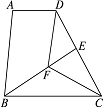
如图,已知在四边形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC
于点E.
求证:(1)△BFC≌△DFC;
(2)AD=DE.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com