
如果三角形有一个边上的中线长恰好等于这个边的长,那么称这个三角形是“有趣三角形”,这条中线为“有趣中线”.如图,在△ABC中,∠C=90°,较短的一条直角边BC=1,且△ABC是“有趣三角形”,求△ABC的“有趣中线”的长.
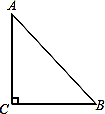
【考点】勾股定理.
【专题】新定义.
【分析】“有趣中线”分三种情况,两个直角边跟斜边,而直角三角形的斜边的中点到三顶点距离相等,不符合;两个直角边,有一种情况有趣中线为1.但是不符合较短的一条直角边边长为1,只能为另一条直角边上的中线,利用勾股定理求出即可.
【解答】解:“有趣中线”有三种情况:
若“有趣中线”为斜边AB上的中线,直角三角形的斜边的中点到三顶点距离相等,不合题意;
若“有趣中线”为BC边上的中线,根据斜边大于直角边,矛盾,不成立;
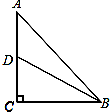
若“有趣中线”为另一直角边AC上的中线,如图所示,BC=1,
设BD=2x,则CD=x,
在Rt△CBD中,根据勾股定理得:BD2=BC2+CD2,即(2x)2=12+x2,
解得:x=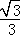 ,
,
则△ABC的“有趣中线”的长等于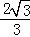 .
.
【点评】此题考查了勾股定理、新定义;熟练掌握新定义,由勾股定理得出方程是解本题的关键,注意分类讨论.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
小明四等分弧AB,他的作法如下:
(1)连接AB(如图);
(2)作AB的垂直平分线CD交弧AB于点M,交AB于点T;
(3)分别作AT,TB的垂直平分线EF,GH,交弧AB于N,P两点,则N,M,P三点把弧AB四等分.
你认为小明的作法是否正确: ,理由是 .
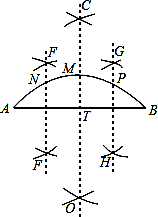
查看答案和解析>>
科目:初中数学 来源: 题型:
.以下列各组线段为边,能组成三角形的是
A.1cm,2cm,3cm B.2cm,3cm,6cm C.8cm,6cm,4cm D.12cm,5cm,6cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com