
【题目】已知点O在直线MN上,过点O作射线OP,使∠MOP=130°,将一块直角三角板的直角顶点始终放在点O处.
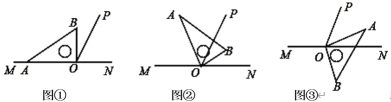
(1)如图①,当三角板的一边OA在射线OM上,另一边OB在直线MN的上方时,求∠POB的度数;
(2)若将三角板绕点O旋转至图②所示的位置,此时OB恰好平分∠PON,求∠BOP和∠AOM 的度数;
(3)若将三角板绕点O旋转至图③所示位置,此时OA在∠PON 的内部,若OP所在的直线平分∠MOB,求∠POA 的度数;
【答案】(1)40°;(2)25°;65°;(3)40°
【解析】
(1)根据题意,∠POB=∠POA-∠AOB代入数据即可求出结论;
(2)根据题意,∠PON=180°-∠POM,又根据角平分线的定义可得∠POB=∠NOB
=![]() ,代入已知即可求解;再根据余角定义求出∠POA的度数;
,代入已知即可求解;再根据余角定义求出∠POA的度数;
(3)从已知条件可得,∠MOE=180°-∠MOP,再根据角平分线的定义得∠MOB=2∠MOE, ∠NOA=180°-∠MOB, ∠AON=90°-∠BON, ∠POB=∠PON-∠AON,代入求值即可.
解:(1)∠POB=∠MOP-∠AOB=130°-90°=40°.
(2)∵∠MON是平角,∠MOP=130°,
∴∠PON=∠MON-∠MOP=180°-130°=50°
∵OB 平分∠PON,
∴∠BOP=![]() ∠PON=25°
∠PON=25°
∵∠AOB=90゜,
∴∠AOP=∠AOB-∠BOP=90°-25°=65°
∴∠MOA=∠MOP-∠AOP=130°-65°=65°;
(3)如图,OE是PO的延长线,
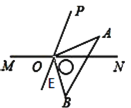
∵∠MOP=130°
∴∠MOE=50°
∵OE是∠MOB的平分线,
∴∠MOB=100°,
∴∠BON=80°
∵∠AOB=90°
∴∠AON=∠AOB-∠BON=90°-80°=10°
∴∠POA=∠PON-∠AON=50°-10°=40°


科目:初中数学 来源: 题型:
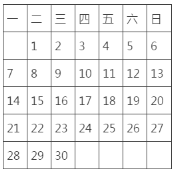
【题目】如图,是某年11月月历
(1)用一个正方形在表中随意框住4个数,把其中最小的记为![]() ,则另外三个可用含
,则另外三个可用含![]() 的式子表示出来,从小到大依次为____________,_____________,_______________.
的式子表示出来,从小到大依次为____________,_____________,_______________.
(2)在(1)中被框住的4个数之和等于76时,则被框住的4个数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】① 如图(1),直线l上有2个点,则图中有2条可用图中字母表示的射线:A1A2、A2A1,有1条线段:A1A2;
② 如图(2),直线l上有3个点,则图中有几条可用图中字母表示的射线,有几条线段,并分别用图中字母表示出来;
③ 如图(3),直线l上有n个点,则图中有多少条可用图中字母表示的射线,有多少条线段,分别用含n的代数式表示出来;
④ 应用(3)中发现的规律解决问题:某校七年级共有8个班进行足球比赛,准备进行循环赛(即每两队之间赛一场),预计全部赛完共需多少场比赛?
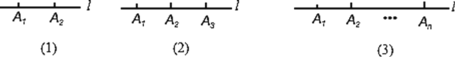
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=3x2+36x+81.
(1)写出它的顶点坐标;
(2)当x取何值时,y随x的增大而增大;
(3)求出图象与x轴的交点坐标;
(4)当x取何值时,y有最小值,并求出最小值;
(5)当x取何值时,y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东方小商品市场一经营者将每件进价为80元的某种小商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种小商品单价每降低1元,其销量可增加10件.
(1)该经营者经营这种商品原来一天可获利润____元;
(2)若设后来该小商品每件降价x元,该经营者一天可获利润y元.
①若该经营者经营该商品一天要获利润2 090元,求每件商品应降价多少元?
②求出y与x之间的函数关系式,并求出当x取何值时,该经营者所获利润最大,且最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB∥CD,点 E 为射线 FG 上一点.
(1)如图 1,若∠EAF=30°,∠EDG=40°,则∠AED= °;
(2)如图 2,当点 E 在 FG 延长线上时,此时 CD 与 AE 交于点 H,则∠AED、∠EAF、∠EDG之间满足怎样的关系,请说明你的结论;
(3)如图 3,DI 平分∠EDC,交 AE 于点 K,交 AI 于点 I,且∠EAI:∠BAI=1:2,∠AED=22°,∠I=20°,求∠EKD 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
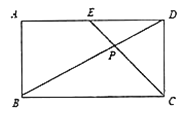
【题目】学完《平面直角坐标系》和《一次函数》这两章后,老师布置了这样一道思考题:已知:如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() 和
和![]() 相交于点
相交于点![]() .求
.求![]() 的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以
的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以![]() 所在的直线为
所在的直线为![]() 轴,以
轴,以![]() 所在的直线为
所在的直线为![]() 轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点
轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点![]() 的坐标,从而求得
的坐标,从而求得![]() 的面积.请你按照小明的思路解决这道思考题.
的面积.请你按照小明的思路解决这道思考题.
查看答案和解析>>
科目:初中数学 来源: 题型:
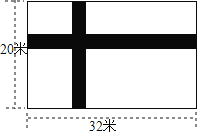
【题目】如图所示,宽为20米,长为32米的长方形地面上,修筑宽度为x米的两条互相垂直的小路,余下的部分作为耕地,如果要在耕地上铺上草皮,选用草皮的价格是每平米a元,
(1)求买草皮至少需要多少元?(用含a,x的式子表示)
(2)计算a=40,x=2时,草皮的费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com