
【题目】如图,长方形ABCD被分成六个小的正方,已知中间一个小正方形的边长为1,其它正方形的边长分别为a、b、c、d.观察图形并探索:(1)b=_____,d=_____;(用含a的代数式表示)(2)长方形ABCD的面积为_____.
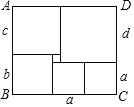
【答案】a+1 2a﹣1 143
【解析】
(1)利用中间一个小正方形的边长为1,得出b,d与a的关系;
(2)利用c=b+1,b=a+1,得出c=a+2,再利用c=d﹣1,d=2a﹣1,得出c=2a﹣2,那么2a﹣2=a+2,解方程求出a的值,然后分别计算出长方形ABCD的长与宽,进而求出面积.
(1)∵中间一个小正方形的边长为1,
∴b=a+1,d=2a﹣1;
故答案为:a+1,2a﹣1;
(2)∵c=b+1,b=a+1,
∴c=a+2,
又∵c=d﹣1,d=2a﹣1,
∴c=2a﹣2,
∴2a﹣2=a+2,
解得a=4.
则长方形ABCD的长为c+d=a+2+2a﹣1=3a+1=13,
宽为a+d=a+2a﹣1=3a﹣1=11,
所以长方形ABCD的面积为:11×13=143.
故答案为:143.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)若k取小于1的整数,且此方程的解为整数,则求出此方程的两个整数根;
(3)在(2)的条件下,二次函数![]() 与x轴交于A、B两点(A点在B点的左侧),D点在此抛物线的对称轴上,若∠DAB=60,直接写出D点的坐标.
与x轴交于A、B两点(A点在B点的左侧),D点在此抛物线的对称轴上,若∠DAB=60,直接写出D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是 ( )

A. AB=CD B. AC=BD C. ∠A=∠D D. ∠ABC=∠DCB
查看答案和解析>>
科目:初中数学 来源: 题型:
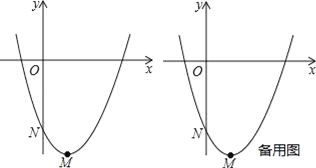
【题目】已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张正面分别标有数字![]() 的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为
的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为![]() ,另有一个被均匀分成4份的转盘,上面分别标有数字
,另有一个被均匀分成4份的转盘,上面分别标有数字![]() ,转动转盘,指针所指的数字记为
,转动转盘,指针所指的数字记为![]() (若指针指在分割线上则重新转一次),则点
(若指针指在分割线上则重新转一次),则点![]() 落在抛物线
落在抛物线![]() 与
与![]() 轴所围成的区域内(不含边界)的概率是__________.
轴所围成的区域内(不含边界)的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:

(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 商品以每件
商品以每件![]() 元出售,
元出售,![]() 商品以每件
商品以每件![]() 元出售.为满足市场需求,需购进
元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共
两种商品共![]() 件,且
件,且![]() 商品的数量不少于
商品的数量不少于![]() 种商品数量的
种商品数量的![]() 倍,请你求出获利最大的进货方案,并确定最大利润.
倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潮州市某学校为了改善办学条件,购置一批电子白板和台式电脑合共24台.经招投标,一台电子白板每台9000元,一台台式电脑每台3000元,设学校购买电子白板和台式电脑总费用为![]() 元,购买了
元,购买了![]() 台电子白板,并且台式电脑的台数不超过电子白板台数的3倍.
台电子白板,并且台式电脑的台数不超过电子白板台数的3倍.
(1)请求出![]() 与
与![]() 的函数解析式,并直接写出
的函数解析式,并直接写出![]() 的取值范围
的取值范围
(2)请问当购买多少台电子白板时,学校购置电子白板和台式电脑的总费用最少,最少多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果 x 与 y 都是整数,就称点(x,y)为整点.下列命题中错误的是( )
A. 存在这样的直线,既不与坐标轴平行,又不经过任何整点
B. 若 k 与 b 都是无理数,则直线 y=kx+b 不经过任何整点
C. 若直线 y=kx+b 经过无数多个整点,则 k 与 b 都是有理数
D. 存在恰好经过一个整点的直线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com