
【题目】如图,△ABC中,AB=AC,∠C=30°,DA⊥BA于A,BC=6cm,求AD的长.

【答案】2
【解析】
根据等边对等角可得∠B=∠C,再利用三角形的内角和定理求出∠BAC=120°,然后求出∠CAD=30°,从而得到∠CAD=∠C,根据等角对等边可得AD=CD,再根据直角三角形30°角所对的直角边等于斜边的一半可得BD=2AD,然后根据BC=BD+CD列出方程求解即可
∵AB=AC,
∴∠B=∠C=30°,
∴∠BAC=180°-2×30°=120°,
∵DA⊥BA,
∴∠BAD=90°,
∴∠CAD=120°-90°=30°,
∴∠CAD=∠C,
∴AD=CD,
在Rt△ABD中,
∵∠B=30°,∠BAD=90°,
∴BD=2AD,
∴BC=BD+CD=2AD+AD=3AD,
∵BC=6cm,
∴AD=2cm.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(![]() )将
)将![]() 化成
化成![]() 的形式.
的形式.
(![]() )与
)与![]() 轴的交点坐标是__________,与
轴的交点坐标是__________,与![]() 轴的交点坐标是__________.
轴的交点坐标是__________.
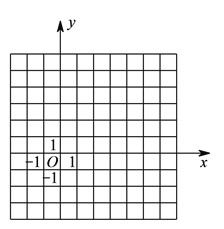
(![]() )在坐标系中利用描点法画出此抛物线.
)在坐标系中利用描点法画出此抛物线.
|
|
| |||||
|
|
|
(![]() )不等式
)不等式![]() 的解集是__________.
的解集是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;②a﹣b+c<0;③当x<1时,y随x增大而增大;
④抛物线的顶点坐标为(2,b);⑤若ax2+bx+c=b,则b2﹣4ac=0.
其中正确的是( )

A. ①②③ B. ①④⑤ C. ①②④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解居民的环保意识,社区工作人员在某小区随机抽取了若干名居民开展有奖问卷调查活动,并用得到的数据绘制了如下条形统计图.请根据图中信息,解答下列问题.

(1)求本次调查获取的样本数据的平均数;
(2)如果对该小区的800名居民全面开展这项有奖问卷活动,得10分者设为一等奖,请你根据调查结果,估计需准备多少份一等奖奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为5,由直径AB的端点B作⊙O的切线,从圆周上一点P引该切线的垂线PM,M为垂足,连接PA,设PA=x,则AP+2PM的函数表达式为______,此函数的最大值是____,最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国的农作物主要以水稻、玉米和小麦为主,种植太单调不利于土壤环境的维护,而且对农业的发展也没有促进作用,为了鼓励大豆的种植,国家对种植大豆的农民给予补贴,调动农民种植大豆的积极性.我市乃大豆之乡,今年很多合作社调整种植结构,把种植玉米改成种植大豆,今年我市某合作社共收获大豆200吨,计划采用批发和零售两种方式销售.经市场调查,批发平均每天售出14吨,由于今年我市小型大豆深加工企业的增多,预计能提前完成销售任务,在平均每天批发量不变的情况下,实际平均每天的零售量比原计划的2倍还多14吨,结果提前5天完成销售任务。那么原计划零售平均每天售出多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员的10次射击训练,成绩分别被制成下列两个统计图.
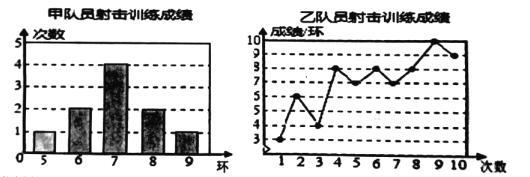
并整理分析数据如下表:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
| 8 |
|
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
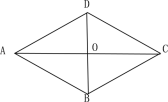
【题目】如图,四边形ABCD是菱形,对角线AC与BD相交于O,∠ACB=30°, BD=12.
(1)求及∠BAD,∠ABC的度数;
(2)求AB、AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 和点
和点![]() ,点
,点![]() 和点
和点![]() 是
是![]() 轴上的两个定点.
轴上的两个定点.
(1)当线段![]() 向左平移到某个位置时,若
向左平移到某个位置时,若![]() 的值最小,求平移的距离.
的值最小,求平移的距离.
(2)当线段![]() 向左或向右平移时,是否存在某个位置,使四边形
向左或向右平移时,是否存在某个位置,使四边形![]() 的周长最小?请说明如何平移?若不存在,请说明理由.
的周长最小?请说明如何平移?若不存在,请说明理由.
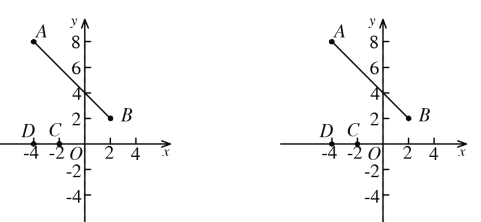
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com