
���� ��1��ֻ����������ƽ�����Ķ���Ϳɽ�����⣻
��2�����ݼ��������Է���һ������ƽ��������ƽ��������������ľ���ֵ��Ȼ������������־Ϳɽ�����⣮
��� �⣺��1��$\sqrt{{2}^{2}}$=2��$\sqrt{2��{5}^{2}}$=2.5��$\sqrt{��-3��^{2}}$=3��$\sqrt{{0}^{2}}$=0��$\sqrt{��\frac{3}{5}��^{2}}$=$\frac{3}{5}$��$\sqrt{��-\frac{2}{3}��^{2}}$=$\frac{2}{3}$��
�ʴ𰸷ֱ�Ϊ��2��2.5��3��0��$\frac{3}{5}$��$\frac{2}{3}$��
��2��$\sqrt{{a}^{2}}$��һ������a���ҷ���һ������ƽ��������ƽ��������������ľ���ֵ��
��$\sqrt{��2-\sqrt{5}��^{2}}$=|2-$\sqrt{5}$|=$\sqrt{5}$-2��
�ڡ�a-4��0����a-3��0��4-a��0��
��$\sqrt{{a}^{2}-6a+9}$+|4-a|=$\sqrt{��a-3��^{2}}$+|4-a|=|a-3|+|4-a|=a-3+a-4=2a-7��
�ʴ�Ϊ��$\sqrt{5}$-2����2a-7��
���� �������ڹ���̽���⣬��Ҫ����������ƽ�����Ķ��塢����ֵ�����֪ʶ�����÷��ֵĹ��ɽ�������ǽ���ڣ�2��С��Ĺؼ���


 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д� ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$��a-4�� | B�� | $\frac{1}{4}$a-2 | C�� | $\frac{1}{4}$a+2 | D�� | $\frac{3}{4}$a+2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
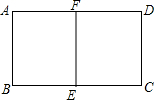 �Ѿ��ζ��ۺ�ԭ���ľ������ƣ���ô������εij�����֮��Ϊ��������
�Ѿ��ζ��ۺ�ԭ���ľ������ƣ���ô������εij�����֮��Ϊ��������| A�� | 2��1 | B�� | 4��1 | C�� | $\sqrt{2}$��1 | D�� | $\frac{3}{2}$��1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com