
【题目】如图,已知AO=OB,OC=OD,AD和BC相交于点E,则图中全等三角形有( )对.
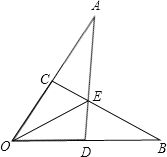
A.1对B.2对C.3对D.4对
科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发负责送货,向东走了2千米到达小明家,继续向东走了4千米到达小红家,然后向西走了9千米到达小刚家,最后返回百货大楼.
(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置;
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油0.5升,那么这辆货车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查.下面是根据收集的数据绘制的两幅不完整的统计图.
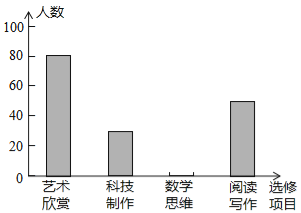
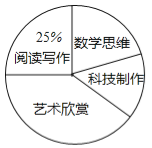
请根据图中提供的信息,解答下面的问题:
(1)此次共调查了 名学生,扇型统计图中“艺术鉴赏”部分的圆心角是 度.
(2)请把这个条形统计图补充完整.
(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修“科技制作”项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(![]() )
)![]() ,正六边形的边长为(
,正六边形的边长为(![]() )cm(其中
)cm(其中![]() ),求这两段铁丝的总长
),求这两段铁丝的总长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知点D,E,F分别为BC,AD,AE的中点,且S△ABC=4cm2,则阴影部分面积S=( )cm2.
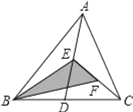
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ABCD 中,AD∥BC,DC⊥BC,将四边形沿对角线 BD 折叠,点 A 恰好落在 DC 边上的 点 A'处,若∠A'BC=20°,则∠A'BD 的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
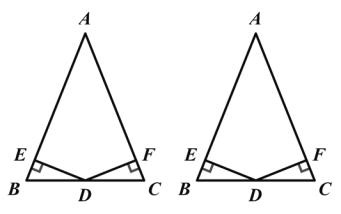
【题目】已知:如图,在△ABC 中,AB=AC,点 D 在 BC 上,DE⊥AB,DF⊥AC,垂足分别为点 E、F,且 DE=DF.
求证:点 D 为 BC 的中点.(请用两种不同的方法证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
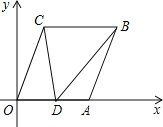
【题目】如图,已知A(6,0),B(8,5),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)求对角线AC的长;
(2)设点D的坐标为(x,0),△ODC与△ABD的面积分别记为S1,S2.设S=S1﹣S2,写出S关于x的函数解析式,并探究是否存在点D使S与△DBC的面积相等?如果存在,用坐标形式写出点D的位置;如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com