
����Ŀ��̽�����֣���ͼ1����ֱ֪��l1��l2����l3��l1��l2�ֱ��ཻ��A��B���㣬l4��l1��l2�ֱ���C��D���㣬��ACP������1����BDP������2����CPD������3����P���߶�AB�ϣ�
��1������1=20�㣬��2=30�㣬���������3�Ķ���
�����ܽ��2����������������⣬�����ҳ�ͼ1�С�1����2����3֮���������ϵ����ֱ��д����Ľ��ۣ�
ʵ��Ӧ�ã���3��Ӧ�ã�2���еĽ��۽���������⣺��ͼ2����A��B�ı�ƫ��40��ķ����ϣ���C�ı�ƫ��45��ķ����ϣ����������������ֱ��д����BAC�Ķ�����
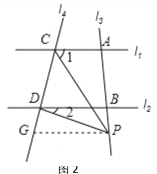
��չ���죺��4�������P��ֱ��l3������A��B��������˶�ʱ�������������䣬��̽����1����2��
��3֮��Ĺ�ϵ����P��A��B���㲻�غϣ���д����Ľ��۲�˵�����ɣ�
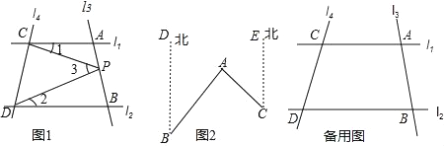
���𰸡���1��500����2����1+��2=��3����3��850����4����P����A�����ʱ����CPD=��2����1����P����B�����ʱ����CPD=��1����2��
�������������������1����P��PM��l1����ͼ��ʾ����l1��l2���õ�PM��l2�����ɵ���1=��CPM=20�㣬��2=��DPM=30�㣬������3=��CPM+��DPM=��1+��2=50�㣻��2����1+��2=��3����ȣ�1�����ɵý��ۣ���3����ȣ�1���ķ�����⼴�ɣ�(4)�ֵ�P����A������뵱P����B���������������з������ۼ���.
���������
��1��500 ��
��2����1+��2=��3��
��3��850
��4����P����A�����ʱ����ͼ1����P��PF��l1����l4��F��
���1=��FPC����l1��l4����PF��l2�����2=��FPD
�ߡ�CPD=��FPD����FPC
���CPD=��2����1��
��P����B�����ʱ����ͼ2����P��PG��l2����l4��G��
���2=��GPD ��l1��l2�� ��PG��l1��
���1=��CPG
�ߡ�CPD=��CPG����GPD
���CPD=��1����2��



 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ƽ��ȥ��һ�������壬�������״�������ǣ� ��
A. ���� B. ������ C. ������ D. �߱���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij����̨��һ��ѡ���Ŀ�У�����λ��ί��ÿλ��ί��ѡ����ɲ��ձ��ݺ�ʾ��ͨ������������ʾ��������̭����������ʾ���������������Ŀ��涨��ÿλѡ�����ٻ����λ��ί����ͨ�������ܽ���
��1����������ͼ�оٳ�ѡ��A�����λ��ί�����ĸ��ֿ��ܵĽ����
��2����ѡ��A�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ������ȷ���ǣ� ��
A. ����3x3��2=9x6 B. ��a��b��2=a2��b2 C. a3a2=a6 D. x2+x2=x4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ó߹������ͼ���������������������Σ������������β���Ψһ���ǣ� ��
A. ��֪������
B. ��֪������
C. ��֪���Ǻͼб�
D. ��֪���ߺͼн�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ε�������нǣ��������������ʱ����һ����ӦΪ�� ��
A. ��һ���߶ε�����֪�߶�
B. ��һ���ǵ�����֪��
C. �������߶ε�����֪�����εıߣ���ʹ��нǵ�����֪��
D. ����һ���߶ε�����֪�߶λ�����һ���ǵ�����֪��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A. ����֮�䣬ֱ����̣�
B. ��һ����һ��ֱ��ƽ������ֱ֪�ߣ�
C. ���������һ��Ƕ�Ӧ��ȵ�����������ȫ�ȣ�
D. ��ƽ���ڹ�һ������ֻ��һ��ֱ�ߴ�ֱ����ֱ֪��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�ļ�����Ϊ37����( )
A. (��3)2��(��3)5 B. (��32)��(��3)5 C. (��3)2��(��35) D. (��3)��(��3)6
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com