Question

18．已知∠A0B=90°，在∠AOB内部引两条射线OC、OD，且∠COD=20°，OM是∠AOC的角平分线，ON是∠BOD的角平分线，∠MON的度数为35°或55°．

Answer 1

分析 分如图所示的两种情况进行解答．由三角形角平分线的性质和角与角间的和差关系进行解答．

解答 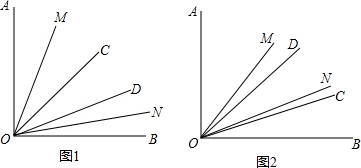解：如图1，∵OM是∠AOC的角平分线，ON是∠BOD的角平分线，
∴∠MOC=$\frac{1}{2}$∠AOC，∠DON=$\frac{1}{2}$∠BOD，
又∵∠COD=20°，
∴∠AOC+∠BOD=70°，
∴∠MON=$\frac{1}{2}$（∠AOC+∠BOD）=35°；
如图2，∵OM是∠AOC的角平分线，ON是∠BOD的角平分线，
∴∠MOC=$\frac{1}{2}$∠AOC，∠DON=$\frac{1}{2}$∠BOD，
又∵∠COD=20°，
∴∠AOC+∠BOD=90°+20°=110°，
∴∠MON=$\frac{1}{2}$（∠AOC+∠BOD）=55°．
综上所述，∠MON的度数为35°或55°．
故答案是：35°或55°．

点评 本题考查了角平分线的定义．解题时要分类讨论，以防漏解．