
【题目】已知:△ABC内接于⊙O,连接AO并延长交BC于点D.
(1)如图1,求证;∠ABC+∠CAD=90°;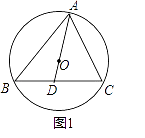

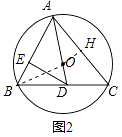
(2)如图2,过点D作DE⊥AB于E,若∠ADC=2∠ACB.求证:AC=2DE;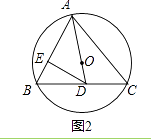
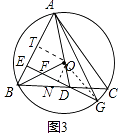
(3)如图3,在(2)的条件下,连接BO交DE于点F,延长ED交⊙O于点G,连接AG,若AC=6 ![]() ,BF=OD,求线段AG的长.
,BF=OD,求线段AG的长.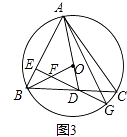
【答案】
(1)
证明:如图1中,延长AD交⊙O于点M,连接MC.
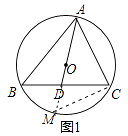
∵AM为⊙O的直径,
∴∠ACM=90°,
∴∠ABC=∠AMC,
∵∠AMC+∠MAC=90°,
∴∠B+∠CAD=90°.
(2)
证明:如图2中,过点O作OH⊥AC于H,连接BO.
∴∠AOB=2∠ACB,
∵∠ADC=2∠ACB,
∴∠AOB=∠ADC,
∴∠BOD=∠BDO,
∴BD=BO,
∵∠BED=∠AHO,∠ABD=∠AOH,
∴△BDE≌△AOH,
∴DE=AH,
∵OH⊥AC,
∴AH=CH= ![]() AC,
AC,
∴AC=2DE.
(3)
证明:如图3中,过点O作ON⊥EG于N,OT⊥AB于T,连接OG.
∵AC=6 ![]() ,AC=2DE,
,AC=2DE,
∴DE=3 ![]() ,
,
∵OA=OB,
∴∠ABO=∠BAO,
∵∠ABO+∠BFE=90°,∠BAO+∠ADE=90°,
∴∠BFE=∠OFD=∠ODF,
∴OF=OD,
∵BF=OD,
∴OF=OD=BF,
∴△BFE≌△OFN,
∴BE=ON EF=FN
∵OF=OD,ON⊥FD,
∴EF=FN=ND= ![]() ,
,
∵BE=ON,OG=BD,
∴△BED≌△NOG,
∴ED=NG,
∴EG=5 ![]() ,
,
∵ON⊥EG OT⊥AB DE⊥AB,
∴四边形ONET为矩形,
∴BE=ET=ON,
∵OT⊥AB,
∴AT=BT,AE=3BE,
设AO=BD=r,OD= ![]() r,AD=
r,AD= ![]() r
r
在Rt△AED中,AE2=AD2﹣ED2,
在Rt△BED中,BE2=BD2﹣ED2,
即( ![]() r)2﹣(3
r)2﹣(3 ![]() )2=9[(
)2=9[( ![]() r)2﹣(3
r)2﹣(3 ![]() )2],
)2],
r=4 ![]() 或r=﹣4
或r=﹣4 ![]() (舍去),
(舍去),
∴AE=15,
在△AEG中,AG= ![]() =10
=10 ![]() .
.
【解析】(1)如图1中,延长AD交⊙O于点M,连接MC.首先证明∠ACM=90°,再证明∠ABC=∠M即可解决问题.(2)如图2中,过点O作OH⊥AC于H,连接BO.想办法证明△BDE≌△AOH即可解决问题.(3)如图3中,过点O作ON⊥EG于N,OT⊥AB于T,连接OG.由△BFE≌△OFN,推出BE=ON EF=FN由OF=OD,ON⊥FD,推出EF=FN=ND= ![]() ,由△BED≌△NOG,推出ED=NG,再证明AE=3BE,设AO=BD=r,OD=
,由△BED≌△NOG,推出ED=NG,再证明AE=3BE,设AO=BD=r,OD= ![]() r,AD=
r,AD= ![]() r在Rt△AED中,AE2=AD2﹣ED2 , 在Rt△BED中,BE2=BD2﹣ED2 , 即(
r在Rt△AED中,AE2=AD2﹣ED2 , 在Rt△BED中,BE2=BD2﹣ED2 , 即( ![]() r)2﹣(3
r)2﹣(3 ![]() )2=9[(
)2=9[( ![]() r)2﹣(3
r)2﹣(3 ![]() )2],求出r即可解决问题.
)2],求出r即可解决问题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】在正六边形ABCDEF中,N、M为边上的点,BM、AN相交于点P
(1)如图1,若点N在边BC上,点M在边DC上,BN=CM,求证:BPBM=BNBC;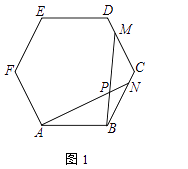
(2)如图2,若N为边DC的中点,M在边ED上,AM∥BN,求 ![]() 的值;
的值;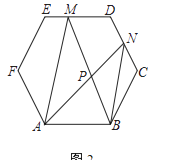
(3)如图3,若N、M分别为边BC、EF的中点,正六边形ABCDEF的边长为2,请直接写出AP的长.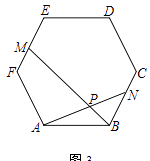
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学为了解该校学生对四种国家一级保护动物的喜爱情况,围绕“在丹顶鹤、大熊猫、滇金丝猴、藏羚羊四种国家一级保护动物中,你最喜欢哪一种动物?(必选且只选一种)”这一问题,在全校范围内随机抽取部分同学进行问卷调查.根据调查结果绘制成如下不完整的条形统计图.其中最喜欢丹顶鹤的学生人数占被抽取人数的16%;请你根据以上信息解答下列问题: 
(1)在这次调查中,一共抽取了多少名学生?
(2)求在被调查的学生中,最喜欢滇金丝猴的学生有多少名?并补全条形统计图;
(3)如果全校有1200名学生,请你估计全校最喜欢大熊猫的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在规格为8×8的边长为1个单位的正方形网格中(每个小正方形的边长为1),△ABC的三个顶点都在格点上,且直线m、n互相垂直.
(1)画出△ABC关于直线n的对称图形△A′B′C′;
(2)直线m上存在一点P,使△APB的周长最小;
①在直线m上作出该点P;(保留画图痕迹)
②△APB的周长的最小值为 .(直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
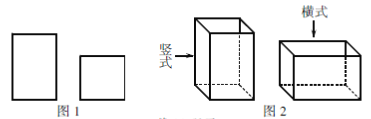
【题目】某商户用如图1的长方形和正方形纸板作侧面和底面(长方形的宽与正方形的边长相等),加工成如图2的竖式与横式两种无盖纸箱. (加工时接缝材料不计)
(1)该商户原计划用若干天加工纸箱300个,后因工作需要,将工作效率提高为原计划的1.8倍,提前4天完成了任务,且总共比原计划多加工纸箱60个,问原计划几天完成工作任务?
(2)若该商户购进正方形纸板450张,长方形纸板1300张. 问竖式纸箱、横式纸箱各加工多少个,恰好能将购进的纸板全部用完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:(只保留作图痕迹)如图,在方格纸中,有两条线段AB、BC.利用方格纸完成以下操作:
(1)过点A作BC的平行线;
(2)过点C作AB的平行线,与(1)中的平行线交于点D;
(3)过点B作AB的垂线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山东全省2016年国庆假期旅游人数增长12.5%,其中尤其是乡村旅游最为火爆.泰山脚下的某旅游村,为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出,若每张床位每天收费提高20元,则相应的减少了10张床位租出,如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A.140元
B.150元
C.160元
D.180元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是( )

A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简![]() ,再任意选一个你喜欢的数作为x的值代入求值.
,再任意选一个你喜欢的数作为x的值代入求值.
(2)先化简,再求值:![]() ,其中a2-a=0.
,其中a2-a=0.
(3)已知y=![]() -x+3.试说明不论x为任何有意义的值,y的值均不变.
-x+3.试说明不论x为任何有意义的值,y的值均不变.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com