
【题目】如图,在平面直角坐标系中,点C的坐标为(0,4),动点A以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.运动时间为t秒.
(1)当点B与点D重合时,求t的值;
(2)设△BCD的面积为S,当t为何值时,S=![]() ?
?
(3)连接MB,当MB∥OA时,如果抛物线y=ax2﹣10ax的顶点在△ABM内部(不包括边),求a的取值范围.
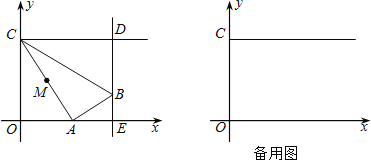
【答案】(1)t=8(2)当t=3或3+5![]() 时,S=
时,S=![]() (3)-
(3)-![]() <a<-
<a<-![]()
【解析】解:(1)∵![]() ,
,![]() ,
,
∴![]() .
.
∴Rt△CAO∽Rt△ABE.·························· 2分
∴![]() .
.
∴![]() .∴
.∴![]() .························· 3分
.························· 3分
(2)由Rt△CAO∽Rt△ABE可知:![]() ,
,![]() .··········· 4分
.··········· 4分
当0<![]() <8时,
<8时,![]() .
.
∴![]() .····························· 6分
.····························· 6分
当![]() >8时,
>8时,![]() .
.
∴![]() ,
,![]() (为负数,舍去).
(为负数,舍去).
当![]() 或
或![]() 时,
时,![]() .······················ 8分
.······················ 8分

(3)过M作MN⊥![]() 轴于N,则
轴于N,则![]() .
.
当MB∥OA时,![]() ,
,![]() .··············· 9分
.··············· 9分
抛物线![]() 的顶点坐标为(5,
的顶点坐标为(5,![]() ).············· 10分
).············· 10分
它的顶点在直线![]() 上移动.
上移动.
直线![]() 交MB于点(5,2),交AB于点(5,1).············· 11分
交MB于点(5,2),交AB于点(5,1).············· 11分
∴1<![]() <2.
<2.
∴![]() <
<![]() <
<![]() . 12分
. 12分


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
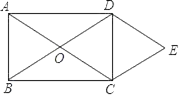
【题目】如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若点E到CD的距离为2,CD=3,试求出矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
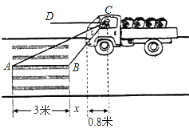
【题目】如图:一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 和一次函数y=-x+a-1(a为常数)
和一次函数y=-x+a-1(a为常数)
(1)当a=5时,求反比例函数与一次函数的交点坐标(5分)
(2)是否存在实数a,使反比例函数与一次函数有且只有一个交点,如果存在,求出实数a,如果不存在,说明理由(5分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度沿负方向运动,动点
个单位长度的速度沿负方向运动,动点![]() 从原点出发以每秒
从原点出发以每秒![]() 个单位长度的速度沿负方向运动,动点
个单位长度的速度沿负方向运动,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位的速度先沿正方向运动,到达原点后立即按原速反方向运动,三点同时出发,出发时间为
个单位的速度先沿正方向运动,到达原点后立即按原速反方向运动,三点同时出发,出发时间为![]() (秒).
(秒).

(1)点![]() 在数轴上所表示的数分别为:____________,____________;
在数轴上所表示的数分别为:____________,____________;
(2)当![]() 两点重合时,求此时点
两点重合时,求此时点![]() 在数轴上所表示的数;
在数轴上所表示的数;
查看答案和解析>>
科目:初中数学 来源: 题型:
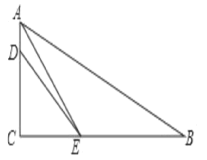
【题目】已知,如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE.
(1)求证:∠B+∠EDA=180°;
(2)求![]() 的值。.
的值。.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依此为2,4,6,8,...,顶点依此用A1,A2,A3,A4......表示,则顶点A55的坐标是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线AB经过点A(﹣2,0),与y轴的正半轴交于点B,且OA=2OB.
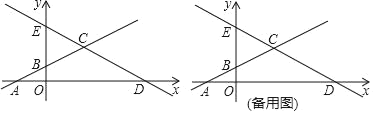
(1)求直线AB的函数表达式;
(2)点C在直线AB上,且BC=AB,点E是y轴上的动点,直线EC交x轴于点D,设点E的坐标为(0,m)(m>2),求点D的坐标(用含m的代数式表示);
(3)在(2)的条件下,若CE:CD=1:2,点F是直线AB上的动点,在直线AC上方的平面内是否存在一点G,使以C,G,F,E为顶点的四边形是菱形?若存在,请求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com