
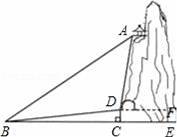
ij��������һ��������������춴��D���Ƕ�����ڣ����˴���ڽ��������ɾ�ɽ������ɽ���ij�����ͤA���ۿ��������羰��������³�������AB����ɽ���µ�B������ͬһƽ���ڣ������б��BD�ij�Ϊ100�ף��½ǡ�DBC=10�㣬��B�����A�����ǡ�ABC=40�㣬��D�����A�����ǡ�ADF=85�㣬��D��������BE�Ĵ��ߣ�����ΪC��
��1�����ADB�Ķ�����
��2��������AB�ij���������������ţ�

��
�����㡿��ֱ�������ε�Ӧ��-���Ǹ������⣮
��ר�⡿ת��˼�룮
����������1�����õ�D�����ܽǼ�����á�ADB�Ķ�����
��2�����ȷ���ͼ�Σ����������ֱ�������Σ������漰������ֱ�������Σ�Ӧ�����乫���߹������ǹ�ϵ������������𰸣�
����𡿽⣺��1����DC��CE��
���BCD=90�㣮
�֡ߡ�DBC=10�㣬
���BDC=80�㣮
�ߡ�ADF=85�㣬
���ADB=360�㩁80�㩁90�㩁85��=105�㣮
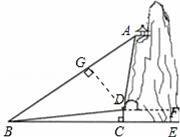
��2������D��DG��AB�ڵ�G��
��Rt��GDB��
��GBD=40�㩁10��=30�㣬
���BDG=90�㩁30��=60�㣮
�֡�BD=100�ף�
��GD=
 BD=100��
BD=100��
 =50�ף�
=50�ף�
��GB=BD��cos30��=100��
 =50
=50
 �ף�
�ף�
��Rt��ADG�У���ADG=105�㩁60��=45�㣬
��GD=GA=50�ף�
��AB=AG+GB=��50+50
 ���ף�
���ף�
����������50+50
 ���ף�
���ף�

�����������⿼�����ǵĶ��弰ֱ�������εĽⷨ�����ȹ���ֱ�������Σ��ٽ����DZ߹�ϵ�����Ǻ����Ķ�����⣮
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���ڱ߳�Ϊ6
 ��������ABCD�У�E��AB����һ�㣬G��AD�ӳ�����һ�㣬BE=DG������EG��CF��EG��EG�ڵ�H����AD�ڵ�F������CE��BH����BH=8����FG=������
��������ABCD�У�E��AB����һ�㣬G��AD�ӳ�����һ�㣬BE=DG������EG��CF��EG��EG�ڵ�H����AD�ڵ�F������CE��BH����BH=8����FG=������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����������ȷ���ǣ�������
A��
 =��3 B��
=��3 B��
 =2
=2
C����x+2y��2=x2+2xy+4y2 D��
 ��
��
 =
=

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ʾ��Rt��ABC��Rt��DEF����cosE��ֵ���ڣ�������


A��
 B��
B��
 C��
C��
 D��
D��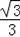

��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���и�ʽ������ȷ���ǣ�������
A��2a2+3a2=5a4 B����2ab2��2=4a2b4 C��2a6��a3=2a2 D����a2��3=a5
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����O��0��0����A��2��0��Ϊ����������OAP1���Ե�P1���߶�P1A���е�BΪ����������P1BP2�����Ե�P2���߶�P2B���е�CΪ��������P2CP3��������˼�����ȥ������������������У����ڵ�������������ϵĶ���P6��������������


��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����▱ABCD�У��Խ���AC��BD�ཻ�ɵ����Ϊ������AC=a��BD=b����▱ABCD������ǣ�������


A��
 absin�� B��absin�� C��abcos�� D��
absin�� B��absin�� C��abcos�� D��
 abcos��
abcos��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����-(-3a2b3) 4�Ľ���ǣ� ��
A. 81a8b12�� B. 12a6b7�� C. -12a6b7�� D. -81a8b12��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com