
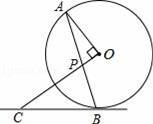
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为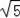
 ,OP=1,求BC的长.
,OP=1,求BC的长.

【考点】切线的判定.
【专题】几何图形问题.
【分析】(1)由垂直定义得∠A+∠APO=90°,根据等腰三角形的性质由CP=CB得∠CBP=∠CPB,根据对顶角相等得∠CPB=∠APO,所以∠APO=∠CBP,而∠A=∠OBA,所以∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,然后根据切线的判定定理得到BC是⊙O的切线;
(2)设BC=x,则PC=x,在Rt△OBC中,根据勾股定理得到(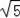
 )2+x2=(x+1)2,然后解方程即可.
)2+x2=(x+1)2,然后解方程即可.
【解答】(1)证明:连接OB,如图,
∵OP⊥OA,
∴∠AOP=90°,
∴∠A+∠APO=90°,
∵CP=CB,
∴∠CBP=∠CPB,
而∠CPB=∠APO,
∴∠APO=∠CBP,
∵OA=OB,
∴∠A=∠OBA,
∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,
∴OB⊥BC,
∴BC是⊙O的切线;
(2)解:设BC=x,则PC=x,
在Rt△OBC中,OB=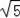
 ,OC=CP+OP=x+1,
,OC=CP+OP=x+1,
∵OB2+BC2=OC2,
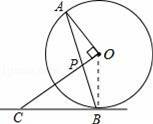
∴(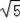
 )2+x2=(x+1)2,
)2+x2=(x+1)2,
解得x=2,
即BC的长为2.

【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了勾股定理.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
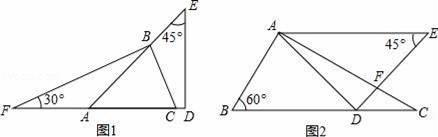
生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:
(1)图1中的∠ABC的度数为 .
(2)图2中已知AE∥BC,则∠AFD的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
“国美商场”销售某品牌汤锅,其成本为每件80元,9月份的销售额为2万元,10月份商场对这种汤锅的售价打9折销售,结果销售量增加了50件,销售额增加了0.7万元.(销售额=销售量×售价)
(1)求“国美商场”9月份销售该品牌汤锅的销售单价;
(2)11月11日“购物节”商场在9月份售价的基础上打折促销(但不亏本),销售的数量y(件)与打折的折数x满足一次函数y=﹣50x+600.问商场打几折时利润最大,最大利润是多少?
(3)在(2)的条件下,为保证“国美商场”利润不低于1.5万元,且能够最大限度帮助厂家减少库存,“国美”商场应该在9月份销售价的基础上打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
花粉的质量很小,一粒某种花粉的质量约为0.000103毫克,那么0.000103可用科学记数法表示为( )
A.10.3×10﹣5 B.1.03×10﹣4 C.0.103×10﹣3 D.1.03×10﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
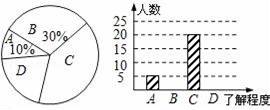
2010年5月1日,第41届世博会在上海举办,世博知识在校园迅速传播.小明同学就本班学生对世博知识的了解程度进行了一次调查统计,下图是他采集数据后绘制的两幅不完整的统计图(A:不了解,B:一般了解,C:了解较多,D:熟悉).请你根据图中提供的信息解答以下问题:
(1)求该班共有多少名学生;
(2)在条形统计图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)从该班中任选一人,其对世博知识的了解程度为“熟悉”的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
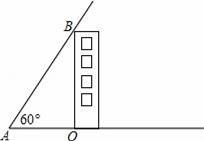
如图,为测量一幢大楼的高度,在地面上距离楼底O点20m的点A处,测得楼顶B点的仰角∠OAB=60°,则这幢大楼的高度为 (用科学计算器计算,结果精确到0.1米).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com