
如图,在⊙O中,O为圆心,点A,B,C在圆上,若OA=AB,则∠ACB=( )
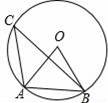

A.15° B.30° C.45° D.60°
科目:初中数学 来源: 题型:
阳光通过窗口AB照射到室内,在地面上留下2.7米的亮区DE(如图所示),已知亮区到窗口下的墙角的距离EC=8.7米,窗口高AB=1.8米,则窗口底边离地面的高BC为( )
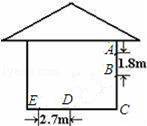

A.4米 B.3.8米 C.3.6米 D.3.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为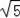
 ,OP=1,求BC的长.
,OP=1,求BC的长.
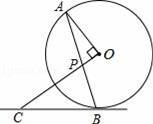

查看答案和解析>>
科目:初中数学 来源: 题型:
一次函数y=﹣x+a﹣3(a为常数)与反比例函数y=﹣
 的图象交于A、B两点,当A、B两点关于原点对称时a的值是( )
的图象交于A、B两点,当A、B两点关于原点对称时a的值是( )
A.0 B.﹣3 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,某古代文物被探明埋于地下的A处,由于点A上方有一些管道,考古人员不能垂直向下挖掘,他们被允许从B处或C处挖掘,从B处挖掘时,最短路线BA与地面所成的锐角是56°,从C处挖掘时,最短路线CA与地面所成的锐角是30°,且BC=20m,若考古人员最终从B处挖掘,求挖掘的最短距离.(参考数据:sin56°=0.83,tan56°≈1.48,
 ≈1.73,结果保留整数)
≈1.73,结果保留整数)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com