[题目]如图.E.F.G.H分别是矩形ABCD各边的中点.AB=6.BC=8.则四边形EFGH的面积是．题目和参考答案——青夏教育精英家教网—

【题目】如图，E，F，G，H分别是矩形ABCD各边的中点，AB=6，BC=8，则四边形EFGH的面积是．

【答案】24
【解析】解：∵E，F，G，H分别是矩形ABCD各边的中点，AB=6，BC=8，
∴AH=DH=BF=CF=8，AE=BE=DG=CG=3．
在△AEH与△DGH中，
∵ ，
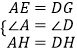∴△AEH≌△DGH（SAS）．
同理可得△AEH≌△DGH≌△CGF≌△BEF，
∴S四边形EFGH=S正方形﹣4S△AEH=6×8﹣4× ×3×4=48﹣24=24．
故答案为：24．
先根据E，F，G，H分别是矩形ABCD各边的中点得出AH=DH=BF=CF，AE=BE=DG=CG，故可得出△AEH≌△DGH≌△CGF≌△BEF，根据S四边形EFGH=S正方形﹣4S△AEH即可得出结论．本题考查的是中点四边形，熟知矩形的对边相等且各角都是直角是解答此题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】矩形纸片ABCD，AB=9，BC=6，在矩形边上有一点P，且DP=3．将矩形纸片折叠，使点B与点P重合，折痕所在直线交矩形两边于点E，F，则EF长为．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】将函数y=2x+b（b为常数）的图象位于x轴下方的部分沿x轴翻折至其上方后，所得的折线是函数y=|2x+b|（b为常数）的图象．若该图象在直线y=2下方的点的横坐标x满足0＜x＜3，则b的取值范围为．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图1，一枚质地均匀的正四面体骰子，它有四个面并分别标有数字1，2，3，4．如图2，正方形ABCD顶点处各有一个圈．跳圈游戏的规则为：游戏者每掷一次骰子，骰子着地一面上的数字是几，就沿正方形的边顺时针方向连续跳几个边长．
如：若从圈A起跳，第一次掷得3，就顺时针连续跳3个边长，落到圈D；若第二次掷得2，就从D开始顺时针连续跳2个边长，落到圈B；…
设游戏者从圈A起跳．

（1）嘉嘉随机掷一次骰子，求落回到圈A的概率P1；
（2）淇淇随机掷两次骰子，用列表法求最后落回到圈A的概率P2 ，并指出她与嘉嘉落回到圈A的可能性一样吗？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在四边形ABCD中，AC平分∠BCD，AC⊥AB，E是BC的中点，AD⊥AE．

（1）求证：AC2=CDBC；
（2）过E作EG⊥AB，并延长EG至点K，使EK=EB．
①若点H是点D关于AC的对称点，点F为AC的中点，求证：FH⊥GH；
②若∠B=30°，求证：四边形AKEC是菱形．