
分析 (1)设第一次每支铅笔进价为x元,则第二次每支铅笔进价为$\frac{5}{4}$x元,根据第二次购进数量比第一次多了50支可列出分式方程解答;
(2)设售价为y元,求出利润表达式,然后列不等式解答.
解答 解:(1)设第一次每支铅笔进价为x元,由题意得:
$\frac{1000}{\frac{5}{4}x}$-$\frac{600}{x}$=50,
解得:x=4,
经检验:x=4是原分式方程的解.
答:第一次每支铅笔的进价为4元.
(2)设售价为y元,第一次每支铅笔的进价为4元,则第二次每支铅笔的进价为0.8×$\frac{5}{4}$=5(元),由题意得:
$\frac{600}{4}$×(y-4)+$\frac{1000}{5}$×(y-5)≥500,
解得y≥6.
答:每支售价至少是6元.
点评 本题考查了分式方程的应用和一元一次不等式的应用,弄清题意并找出题中的数量关系并列出方程是解题的关键.最后不要忘记检验.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
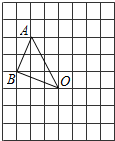 如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为A(-2,3)、B(-3,1).
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为A(-2,3)、B(-3,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com