
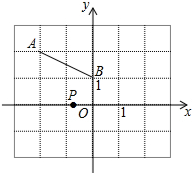
 如图,直角坐标系中,点A(-2,2)、B(0,1),点P在x轴上,且△PAB是等腰三角形,则满足条件的点P共4 个.
如图,直角坐标系中,点A(-2,2)、B(0,1),点P在x轴上,且△PAB是等腰三角形,则满足条件的点P共4 个. 分析 由AB=AP,可得以A为圆心,AB为半径画圆,交x轴有二点P1(-1,0),P2(-3,0);
由BP=AB,可得以B为圆心,BA为半径画圆,交x轴有二点P3(-2,0),(2,0)不能组成△ABP,
由AP=BP,可得AB的垂直平分线交x轴一点P4(PA=PB).
解答 解:如图,点A(-2,2)、B(0,1),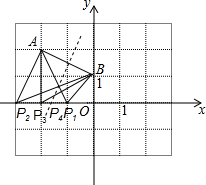
①以A为圆心,AB为半径画圆,交x轴有二点P1(-1,0),P2(-3,0),此时(AP=AB);
②以B为圆心,BA为半径画圆,交x轴有二点P3(-2,0),(2,0)不能组成△ABP,故舍去,此时(BP=AB);
③AB的垂直平分线交x轴一点P4(PA=PB),此时(AP=BP);
设此时P4(x,0),
则(x+2)2+4=x2+1,
解得:x=-$\frac{7}{4}$,
∴P4(-$\frac{7}{4}$,0).
∴符合条件的点有4个.
故答案为4.
点评 此题考查了等腰三角形的判定.此题那难度适中,注意掌握数形结合思想与分类讨论思想的应用.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点O在直线AB上,OD是∠AOC的平分线,射线OE在∠BOC内.
如图,点O在直线AB上,OD是∠AOC的平分线,射线OE在∠BOC内.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x^6}{x^2}={x^3}$ | B. | $\frac{x+m}{x+n}=\frac{m}{n}$ | C. | $\frac{-a+b}{c}=-\frac{a+b}{c}$ | D. | $\frac{1}{a}+\frac{1}{b}=\frac{a+b}{ab}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com