
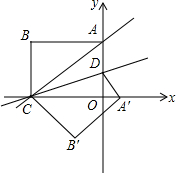
 ��ͼ������AOCB��ֱ������ϵ�У�OΪԭ�㣬C��x���ϣ�A��y���ϣ�ֱ��AC�Ĺ�ϵʽΪy=$\frac{3}{4}$x+9��D��OA�ϵ�һ�㣬��������AOCB��CD�۵�����Aǡ������x���ϵ�A�䴦��
��ͼ������AOCB��ֱ������ϵ�У�OΪԭ�㣬C��x���ϣ�A��y���ϣ�ֱ��AC�Ĺ�ϵʽΪy=$\frac{3}{4}$x+9��D��OA�ϵ�һ�㣬��������AOCB��CD�۵�����Aǡ������x���ϵ�A�䴦������ ��1���������A��C�����꣬Ȼ�����ù��ɶ���������⣻
��2�����ݶԳƵ����ʿɵ�CA'=CA���������A'�����꣬��D��O��n������RT��A��OD�У����ù��ɶ��������з������n��ֵ��Ȼ�����ô���ϵ����������⣻
��3������BE��AC�ڵ�E����BC=BPʱ��t=2CE�����������ε������ʽ�������CE�ij����Ӷ���⣻
��CD�ǡ�ACA'�Ľ�ƽ���ߣ���P��AC�ľ�����ڵ�x��ľ��룬��PΪԲ�ĵġ�P����AC��������OA�ཻ����P��������ľ���ֵ���ں�����ľ���ֵ���ݴ˼����в���ʽ��⣮
��� �⣺��1����ֱ��AC��֪��A��0��9����C��-12��0����
��AC=$\sqrt{1{2}^{2}+{9}^{2}}$=15��
��2����A����A�����ֱ��CD�ĶԳƵ㣬
��AC=A��C��
��A��C=15��
��OA��=15-12=3��
��D��O��n����
��OD=n��A��D=AD=9-n��
��RT��A��OD��A��D2=OA��2+OD2��
����9-n��2=42+n2�����n=$\frac{65}{18}$��
��D��0��$\frac{65}{18}$��
��A�䣨4��0����
��ֱ��A'D�Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{b=\frac{65}{18}}\\{4k+b=0}\end{array}\right.$���$\left\{\begin{array}{l}{k=-\frac{65}{72}}\\{b=\frac{65}{18}}\end{array}\right.$��
��ֱ��A��D�Ĺ�ϵʽ��y=-$\frac{65}{72}$x+$\frac{65}{18}$��
��3������BE��AC�ڵ�E��
��S��ABC=$\frac{1}{2}$AC•BE=$\frac{1}{2}$AB•BC��
��BE=$\frac{AB•BC}{AC}$=$\frac{9��12}{15}$=$\frac{36}{5}$��
��t=2��$\frac{36}{5}$=$\frac{72}{5}$��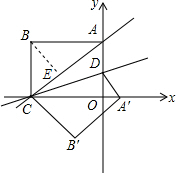 ����CD�Ľ���ʽ��y=kx+b��
����CD�Ľ���ʽ��y=kx+b��
��������ã�$\left\{\begin{array}{l}{-12k+b=0}\\{b=\frac{65}{18}}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{65}{216}}\\{b=\frac{65}{18}}\end{array}\right.$��
��ֱ��CD�Ľ���ʽ��y=$\frac{65}{216}$x+$\frac{65}{18}$��
��-12��x��0ʱ������PΪԲ�ĵġ�P����AC��������OA�ཻʱ��y��-x����$\frac{65}{216}x+\frac{65}{18}$��-x��
��ã�x��-$\frac{780}{281}$��
���ʱx�ķ�Χ�ǣ�-$\frac{780}{281}$��x��0��
��x��0ʱ������PΪԲ�ĵġ�P����AC��������OA�ཻʱ��y��x����$\frac{65}{216}x+\frac{65}{18}$��x��
��ã�x��$\frac{780}{151}$��
��0��x��$\frac{780}{151}$��
��֮��x�ķ�Χ�ǣ�-$\frac{780}{281}$��x��$\frac{780}{151}$��
���� ���⿼���˴���ϵ���������Ľ���ʽ���Լ�ͼ�ε��۵������ʣ�ֱ�ߺ�Բ��λ�ù�ϵ���ж���������PΪԲ�ĵġ�P����AC��������OA�ཻ����P��������ľ���ֵ���ں�����ľ���ֵ�ǹؼ���


 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 13 | B�� | -1 | C�� | -$\frac{7}{3}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����MON=30�㣬��A1��A2��A3��������ON�ϣ���B1��B2��B3��������OM�ϣ���A1B1A2����A2B2A3����A3B3A4����Ϊ�ȱ������Σ��������1���ȱ������εı߳���a1����2���ȱ������εij���Ϊa2���Դ����ƣ���OA1=3����a2=6��a2015=3��22014��
��ͼ����MON=30�㣬��A1��A2��A3��������ON�ϣ���B1��B2��B3��������OM�ϣ���A1B1A2����A2B2A3����A3B3A4����Ϊ�ȱ������Σ��������1���ȱ������εı߳���a1����2���ȱ������εij���Ϊa2���Դ����ƣ���OA1=3����a2=6��a2015=3��22014���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �������n�� | 2 | 3 | 4 | 5 | 6 |
| �������� | 1 | 3 | 6 | 10 | 15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
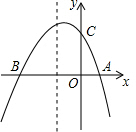 ��ͼ����֪������y=ax2+bx+c��x�ύ��A��m��0����B��n��0������Aλ�ڵ�B���Ҳ࣬��m��n��һԪ���η���x2+2x-3=0������������y�ύ��C��0��3������P���������ϣ���Q��x���ϣ��Ƿ�����Ե�P��Q��A��CΪ������ı�����ƽ���ı��Σ������ڣ������P��Q�����ꣻ�������ڣ���˵�����ɣ�
��ͼ����֪������y=ax2+bx+c��x�ύ��A��m��0����B��n��0������Aλ�ڵ�B���Ҳ࣬��m��n��һԪ���η���x2+2x-3=0������������y�ύ��C��0��3������P���������ϣ���Q��x���ϣ��Ƿ�����Ե�P��Q��A��CΪ������ı�����ƽ���ı��Σ������ڣ������P��Q�����ꣻ�������ڣ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com