
【题目】在平面直角坐标系![]() 中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作
中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作![]() .
.
(1)已知点![]() ,
,
①直接写出![]() 的值;
的值;
②直线![]() 与x轴交于点F,当
与x轴交于点F,当![]() 取最小值时,求k的取值范围;
取最小值时,求k的取值范围;
(2)![]() 的圆心为
的圆心为![]() ,半径为1.若
,半径为1.若![]() ,直接写出t的取值范围.
,直接写出t的取值范围.
【答案】(1)①5.②见解析;(2)![]() .
.
【解析】
(1) ①根据题意![]() 是指点
是指点![]() 到正方形
到正方形![]() 上动点
上动点![]() 的最大距离,所以当点
的最大距离,所以当点![]() 与点
与点![]() 重合时,此时
重合时,此时![]() 最大为
最大为![]() ;
;
②根据![]() 的最小值是,可知
的最小值是,可知![]() ,所以当直线
,所以当直线![]() 经过
经过![]() 和
和![]() ,即可求出
,即可求出![]() 的值;
的值;
(2)根据圆心![]() ,半径为
,半径为![]() ,可知圆
,可知圆![]() 在直线
在直线![]() 的直线上动,因为
的直线上动,因为![]() 圆上动点
圆上动点![]() 到正方形边上动点
到正方形边上动点![]() 的最大值,所以可以转化成
的最大值,所以可以转化成 ![]() 圆的半径
圆的半径![]() 圆心
圆心![]() 到正方形边上动点
到正方形边上动点![]() ,因为
,因为![]() ,可以算出
,可以算出![]() 的分界点,由于圆心
的分界点,由于圆心![]() 到点Q的最大值存在一种情况
到点Q的最大值存在一种情况![]() 时,可以计算出
时,可以计算出![]() ,刚好
,刚好![]() ,即可求出符合题意
,即可求出符合题意![]() 的取值范围.
的取值范围.
解:1.①由根据题意![]() 是指点
是指点![]() 到正方形
到正方形![]() 上动点
上动点![]() 的最大距离,所以当点
的最大距离,所以当点![]() 与点
与点![]() 重合时,此时
重合时,此时![]() 最大,即
最大,即![]()
②如图所示:
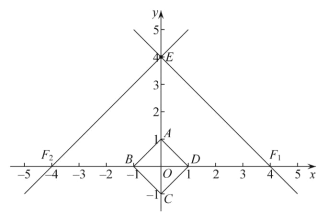
∵![]() .
.
当点![]() 的横坐标在
的横坐标在![]() 时,
时,![]() ,
,
当点![]() 的横坐标在
的横坐标在![]() 时,
时,![]() ,
,
∵![]() 要取最小值,
要取最小值,
∴![]()
∴符合题意的点F满足![]()
∴当直线![]() 经过点
经过点![]() 的坐标为
的坐标为![]() 和点
和点![]() 的坐标为
的坐标为![]() 是分别求得
是分别求得![]() .
.
∴![]() 或
或![]() .
.
结合函数图象可得![]() 或
或![]() .
.
(2)由题意可知:![]()
![]()
![]() 时
时
![]() 可计算当
可计算当![]() 时,
时,
当圆心![]() 在
在![]() 轴左侧时
轴左侧时
![]() 可以考虑到当
可以考虑到当![]() 时,
时,
利用两点之间的距离公式:
即![]()
求得:![]() ,
,
![]()
![]() 当
当![]() 时,
时,![]() ,即
,即![]()
当圆心![]() 在
在![]() 轴右侧时
轴右侧时
![]() 可以考虑到当
可以考虑到当![]() 时,
时,
利用两点之间的距离公式:
即![]()
求得:![]() ,
,
![]()
![]() 当
当![]() 时,
时,![]() ,即
,即![]()
![]()
![]()
![]()
![]()


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示,则下列结论:
之间,其部分图象如图所示,则下列结论:
![]() ;
;
![]() ;
;
![]() 点
点![]() 、
、![]() 、
、![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;
;
![]() ;
;
![]() (
(![]() 为任意实数).
为任意实数).
其中正确结论的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过点
过点![]() 和点
和点![]() ,连结AB交y轴于点C.
,连结AB交y轴于点C.
(1)求抛物线的函数解析式;
(2)点P在线段AB下方的抛物线上运动,连结AP,BP. 设点P的横坐标为m,△ABP的面积为s.
①求s与m的函数关系式;
②当s取最大值时,抛物线上是否存在点Q,使得S△ACQ=s. 若存在,求点Q的坐标;若不存在,说明理由.
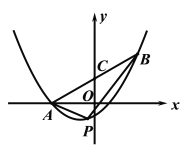
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC的距离分别为h1,h2,h3,△ABC的高为h.
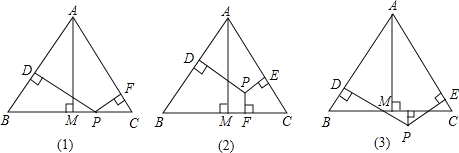
(1)若点P在一边BC上,如图①,此时h3=0,求证:h1+h2+h3=h;
(2)当点P在△ABC内,如图②,以及点P在△ABC外,如图③,这两种情况时,上述结论是否成立?若成立,请予以证明;若不成立,h1,h2,h3与h之间又有怎样的关系,请说出你的猜想,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 经过原点且与两坐标轴分别交于点
经过原点且与两坐标轴分别交于点![]() 和点
和点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,解答下列各题:
,解答下列各题:
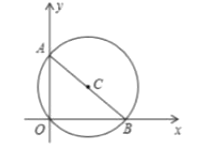
(1)求圆心![]() 的坐标;
的坐标;
(2)在![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 是等腰三角形?若存在,请求出
是等腰三角形?若存在,请求出![]() 的度数;若不存在,请说明理由.
的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励节能降耗,某市规定如下用电收费标准:每户每月的用电量不超过120度时,电价为a元/度;超过120度时,不超过部分仍为a元/度,超过部分为b元/度.已知某用户五月份用电115度,交电费69元,六月份用电140度,交电费94元.
(1)求a,b的值;
(2)设该用户每月用电量为x(度),应付电费为y(元);
①分别求出0≤x≤120和x>120时,y与x之间的函数关系式;
②若该用户计划七月份所付电费不超过83元,问该用户七月份最多可用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2-4ax+c(a≠0)与y轴交于点A,将点A向右平移2个单位长度,得到点B.直线![]() 与x轴,y轴分别交于点C,D.
与x轴,y轴分别交于点C,D.
(1)求抛物线的对称轴.
(2)若点A与点D关于x轴对称.
①求点B的坐标.
②若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里面有13个完全相同的小球,在每一个小球上书写一个汉字,这些汉字组成一句话:“知之为知之,不知为不知,是知也”.随机摸出一个小球然后放回,再随机摸取一个小球,两次取出的小球都是“知”的概率是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com