
ЁОЬтФПЁПФГЩчЧјзщжЏСЫвдЁАБМЯђавИЃЃЌЁЎыІЁЏВНШчЗЩЁБЮЊжїЬтЕФЬпыІзгБШШќЛюЖЏЃЌГѕШќНсЪјКѓгаМзЁЂввСНИіДњБэЖгНјШыОіШќЃЌвбжЊУПЖгга5УћЖгдБЃЌАДЭХЬхзмЪ§ХХСаУћДЮЃЌдкЙцЖЈЪБМфФкУПШЫЬп100ИівдЩЯ(КЌ100)ЮЊгХауЃЎЯТБэЪЧСНЖгИїЖгдБЕФБШШќГЩМЈЃЎ
1 КХ | 2 КХ | 3 КХ | 4 КХ | 5 КХ | змЪ§ | |
МзЖг | 103 | 102 | 98 | 100 | 97 | 500 |
ввЖг | 97 | 99 | 100 | 96 | 108 | 500 |
ОЭГМЦЗЂЯжСНЖг5УћЖгдБЬпыІзгЕФзмИіЪ§ЯрЕШЃЌАДееБШШќЙцдђЃЌСНЖгЛёЕУВЂСаЕквЛЃЎбЇЯАЭГМЦжЊЪЖКѓЃЌЮвУЧПЩвдЭЈЙ§ПМВщЪ§ОнжаЕФЦфЫќаХЯЂзїЮЊВЮПМЃЌНјаазлКЯЦРЖЈЃК
ЃЈ1ЃЉМзЁЂввСНЖгЕФгХауТЪЗжБ№ЮЊЁЁЁЁЁЁЁЁЃЛ
ЃЈ2ЃЉМзЖгБШШќЪ§ОнЕФжаЮЛЪ§ЮЊЁЁЁЁЁЁЁЁИіЃЛввЖгБШШќЪ§ОнЕФжаЮЛЪ§ЮЊЁЁЁЁЁЁЁЁИіЃЛ
ЃЈ3ЃЉЗжБ№МЦЫуМзЁЂввСНЖгБШШќЪ§ОнЕФЗНВюЃЛ
ЃЈ4ЃЉИљОнвдЩЯаХЯЂЃЌФуШЯЮЊзлКЯЦРЖЈФФвЛИіЖгЕФГЩМЈКУЃПМђЪіРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ60%ЃЌ40%ЃЛЃЈ2ЃЉ100ЃЌ99ЃЛЃЈ3ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ4ЃЉзлКЯЦРЖЈМзЖгЕФГЩМЈКУЃЎРэгЩМћНтЮіЃЎ
ЃЛЃЈ4ЃЉзлКЯЦРЖЈМзЖгЕФГЩМЈКУЃЎРэгЩМћНтЮіЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЗжБ№ШУМзввСНЖгЕФгХауИіЪ§Г§вдзмЪ§МДПЩЕУЕУСНЖгЕФгХауТЪЃЛ
ЃЈ2ЃЉИљОнжаЮЛЪ§ЕФЧѓЗЈЗжБ№ЧѓЕУМзввСНЖгЕФжаЮЛЪ§МДПЩЃЛ
ЃЈ3ЃЉИљОнЗНВюЕФЧѓЗЈЗжБ№ЧѓЕУМзввСНЖгЕФЗНВюМДПЩЃЛ
ЃЈ4ЃЉНсКЯЃЈ1ЃЉЁЂЃЈ2ЃЉЁЂЃЈ3ЃЉЕФНсТлНјааЗжЮіХаЖЯМДПЩЃЎ
НтЃКЃЈ1ЃЉЁпМзЖггХауГЩМЈгаШ§ИіЃЌввЖггХауГЩМЈгаЖўИі
Ёр![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпМзввСНЖгГЩМЈЕФЪ§ОнЗжБ№гЩаЁЕНДѓХХађЮЊЃК![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЛ
ЃЛ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]()
ЁрМзввСНЖгЕФжаЮЛЪ§ЗжБ№ЪЧ![]() ЁЂ
ЁЂ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЁпМзЁЂввСНЖгБШШќЪ§ОнЕФЦНОљЪ§ОљЮЊ![]() (Иі)
(Иі)
Ёр![]()
![]() ЃЛ
ЃЛ
ЃЈ4ЃЉзлКЯЦРЖЈМзЖгЕФГЩМЈКУЃЎ
РэгЩШчЯТЃКвђЮЊМзЖгЕФгХауТЪБШввЖгИпЃЛМзЖгЕФжаЮЛЪ§БШввЖгДѓЃЛМзАрЕФЗНВюБШввАрЕЭЃЌБШНЯЮШЖЈЃЌзлКЯЦРЖЈМзЖгБШНЯКУЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
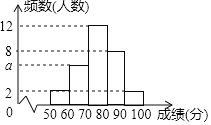
ЁОЬтФПЁПЮЊСЫНтФГДЮЁАаЁбЇЩњЪщЗЈБШШќЁБЕФГЩМЈЧщПіЃЌЫцЛњГщШЁСЫ30УћбЇЩњЕФГЩМЈНјааЭГМЦЃЌВЂНЋЭГМЦЧщПіЛцГЩШчЭМЫљЪОЕФЦЕЪ§ЗжВМжБЗНЭМЃЌМКжЊГЩМЈxЃЈЕЅЮЛЃКЗжЃЉОљТњзуЁА50ЁмxЃМ100ЁБЃЎИљОнЭМжааХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЭМжаaЕФжЕЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєвЊЛцжЦИУбљБОЕФЩШаЮЭГМЦЭМЃЌдђГЩМЈxдкЁА70ЁмxЃМ80ЁБЫљЖдгІЩШаЮЕФдВаФНЧЖШЪ§ЮЊЁЁ ЁЁЖШЃЛ
ЃЈ3ЃЉДЫДЮБШШќЙВга300УћбЇЩњВЮМгЃЌШєНЋЁАxЁн80ЁБЕФГЩМЈМЧЮЊЁАгХауЁБЃЌдђЛёЕУЁАгХауЁАЕФбЇЩњДѓдМгаЁЁ ЁЁШЫЃК
ЃЈ4ЃЉдкетаЉГщВщЕФбљБОжаЃЌаЁУїЕФГЩМЈЮЊ92ЗжЃЌШєДгГЩМЈдкЁА50ЁмxЃМ60ЁБКЭЁА90ЁмxЃМ100ЁБЕФбЇЩњжаШЮбЁ2ШЫЃЌЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓаЁУїБЛбЁжаЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНax2Љ2axЉ2ЕФЭМЯѓЃЈМЧЮЊХзЮяЯпC1ЃЉЖЅЕуЮЊMЃЌжБЯпlЃКyЃН2xЉaгыxжсЃЌyжсЗжБ№НЛгкAЃЌBЃЎ
ЃЈ1ЃЉЖдгкХзЮяЯпC1ЃЌвдЯТНсТле§ШЗЕФЪЧЁЁ ЁЁЃЛ
ЂйЖдГЦжсЪЧЃКжБЯпxЃН1ЃЛЂкЖЅЕузјБъЃЈ1ЃЌЉaЉ2ЃЉЃЛЂлХзЮяЯпвЛЖЈОЙ§СНИіЖЈЕуЃЎ
ЃЈ2ЃЉЕБaЃО0ЪБЃЌЩшЁїABMЕФУцЛ§ЮЊSЃЌЧѓSгыaЕФКЏЪ§ЙиЯЕЃЛ
ЃЈ3ЃЉНЋЖўДЮКЏЪ§yЃНax2Љ2axЉ2ЕФЭМЯѓC1ШЦЕуPЃЈtЃЌЉ2ЃЉа§зЊ180ЁуЕУЕНЖўДЮКЏЪ§ЕФЭМЯѓЃЈМЧЮЊХзЮяЯпC2ЃЉЃЌЖЅЕуЮЊNЃЎ
ЂйЕБЉ2ЁмxЁм1ЪБЃЌа§зЊЧАКѓЕФСНИіЖўДЮКЏЪ§yЕФжЕЖМЛсЫцxЕФдіДѓЖјМѕаЁЃЌЧѓtЕФШЁжЕЗЖЮЇЃЛ
ЂкЕБaЃН1ЪБЃЌЕуQЪЧХзЮяЯпC1ЩЯЕФвЛЕуЃЌЕуQдкХзЮяЯпC2ЩЯЕФЖдгІЕуЮЊQ'ЃЌЪдЬНОПЫФБпаЮQMQ'NФмЗёЮЊе§ЗНаЮЃПШєФмЃЌЧѓГіtЕФжЕЃЌШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭМ1ЪЧФГдЁЪвЛЈШїЪЕОАЭМЃЌЭМ2ЪЧИУЛЈШїЕФВрУцЪОвтЭМЃЎвбжЊЛюЖЏЕїНкЕуBПЩвдЩЯЯТЕїећИпЖШЃЌРыЕиУцCDЕФОрРыBCЃН160cmЃЎЩшЛЈШїБлгыЧНУцЕФМаНЧЮЊІСЃЌПЩвдХЄЖЏЛЈШїБлЕїећНЧЖШЃЌЧвЛЈШїБлГЄABЃН30cmЃЎМйЩшЫЎжљAEДЙжБABжБЯпХчЩфЃЌаЁЛЊдкРыЧНУцОрРыCDЃН120cmДІСмдЁЃЎ

ЃЈ1ЃЉЕБІСЃН30ЁуЪБЃЌЫЎжље§КУТфдкаЁЛЊЕФЭЗЖЅЩЯЃЌЧѓаЁЛЊЕФЩэИпDEЃЎ
ЃЈ2ЃЉШчЙћаЁЛЊвЊЯДНХЃЌашвЊЕїећЫЎжљAEЃЌЪЙЕуEгыЕуDжиКЯЃЌЕїећЕФЗНЪНгаСНжжЃК
ЂйЦфЫћЬѕМўВЛБфЃЌжЛвЊАбЛюЖЏЕїНкЕуBЯђЯТвЦЖЏМДПЩЃЌвЦЖЏЕФОрРыBFгыаЁЛЊЕФЩэИпDEгаЪВУДЪ§СПЙиЯЕЃПжБНгаДГіФуЕФНсТлЃЛ
ЂкЛюЖЏЕїНкЕуBВЛЖЏЃЌжЛвЊЕїећІСЕФДѓаЁЃЌдкЭМ3жаЃЌЪдЧѓІСЕФЖШЪ§ЃЎ
ЃЈВЮПМЪ§ОнЃК![]() Ёж1.73ЃЌsin8.6ЁуЁж0.15ЃЌsin36.9ЁуЁж0.60ЃЌtan36.9ЁуЁж0.75ЃЉ
Ёж1.73ЃЌsin8.6ЁуЁж0.15ЃЌsin36.9ЁуЁж0.60ЃЌtan36.9ЁуЁж0.75ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
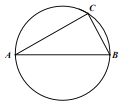
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCМАЦфЭтНгдВЃЌЁЯC=90ЁуЃЌAC=10ЃЎ
(1)ШєИУдВЕФАыОЖЮЊ5![]() ЃЌЧѓЁЯAЕФЖШЪ§ЃЛ
ЃЌЧѓЁЯAЕФЖШЪ§ЃЛ
(2)ЕуMдкABБпЩЯ(AMЃОBM)ЃЌСЌНгCMВЂбгГЄНЛИУдВгкЕуDЃЌСЌНгDBЃЌЙ§ЕуCзїCEДЙжБDBЕФбгГЄЯпгкEЃЎШєBE=3ЃЌCE=4ЃЌЪдХаЖЯABгыCDЪЧЗёЛЅЯрДЙжБЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
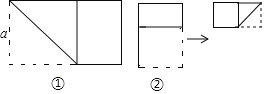
ЁОЬтФПЁПНЋГЄЮЊ2ЁЂПэЮЊaЃЈaДѓгк1ЧваЁгк2ЃЉЕФГЄЗНаЮжНЦЌАДШчЭМЂйЫљЪОЕФЗНЪНелЕўВЂбЙЦНЃЌМєЯТвЛИіБпГЄЕШгкГЄЗНаЮПэЕФе§ЗНаЮЃЌГЦЮЊЕквЛДЮВйзїЃКдйАбЪЃЯТЕФГЄЗНаЮАДШчЭМЂкЫљЪОЕФЗНЪНелЕўВЂбЙЦНЃЌМєЯТИіБпГЄЕШгкДЫЪБГЄЗНаЮПэЕФе§ЗНаЮЃЌГЦЮЊЕкЖўДЮВйзїЃКШчДЫЗДИДВйзїЯТШЅЁЃЌШєдкЕкnДЮВйзїКѓЃЌЪЃЯТЕФГЄЗНаЮЧЁЮЊе§ЗНаЮЃЌдђВйзїжежЙЕБn=3ЪБЃЌaЕФжЕЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
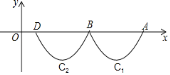
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гыxжсНЛгкЕуAЁЂBЃЌАбХзЮяЯпдкxжсМАЦфЯТЗНЕФВПЗжМЧзїC1ЃЌНЋC1ЯђзѓЦНвЦЕУЕНC2ЃЌC2гыxжсНЛгкЕуBЁЂDЃЌШєжБЯпyЃН
гыxжсНЛгкЕуAЁЂBЃЌАбХзЮяЯпдкxжсМАЦфЯТЗНЕФВПЗжМЧзїC1ЃЌНЋC1ЯђзѓЦНвЦЕУЕНC2ЃЌC2гыxжсНЛгкЕуBЁЂDЃЌШєжБЯпyЃН![]() x+mгыC1ЁЂC2ЙВга3ИіВЛЭЌЕФНЛЕуЃЌдђmЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
x+mгыC1ЁЂC2ЙВга3ИіВЛЭЌЕФНЛЕуЃЌдђmЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжЃжнЪаОЋзМЗіЦЖЙЄзївбНјШыЙЅМсНзЖЮЃЎЦЖРЇЛЇеХВЎВЎдкЯрЙиЕЅЮЛЕФАяЗіЯТАбвЛЦЌЦТЕиИФдьКѓжжжВСЫгХжЪЫЎЙћРЖнЎЃЌНёФъе§ЪНЩЯЪаЯњЪлдкЯњЪлЕФ30ЬьжаЃЌЕквЛЬьТєГі20ЧЇПЫЮЊСЫРЉДѓЯњСПВЩШЁСЫНЕМлДыЪЉвдКѓУПЬьБШЧАвЛЬьЖрТєГі4ЧЇПЫЕк![]() ЬьЕФЪлМлЮЊ
ЬьЕФЪлМлЮЊ![]() дЊ/ЧЇПЫЃЌ
дЊ/ЧЇПЫЃЌ![]() Йигк
Йигк![]() ЕФКЏЪ§НтЮіЪНЮЊ
ЕФКЏЪ§НтЮіЪНЮЊ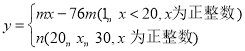 ЃЌЧвЕк12ЬьЕФЪлМлЮЊ32дЊ/ЧЇПЫЃЌЕк26ЬьЕФЪлМлЮЊ25дЊ/ЧЇПЫЃЎвбжЊжжжВЯњЪлРЖнЎЕФГЩБОЪЧ18дЊ/ЧЇПЫЃЌУПЬьЕФРћШѓЪЧ
ЃЌЧвЕк12ЬьЕФЪлМлЮЊ32дЊ/ЧЇПЫЃЌЕк26ЬьЕФЪлМлЮЊ25дЊ/ЧЇПЫЃЎвбжЊжжжВЯњЪлРЖнЎЕФГЩБОЪЧ18дЊ/ЧЇПЫЃЌУПЬьЕФРћШѓЪЧ![]() дЊЃЈРћШѓ=ЯњЪлЪеШы
дЊЃЈРћШѓ=ЯњЪлЪеШы![]() ГЩБОЃЉЃЎ
ГЩБОЃЉЃЎ
ЃЈ1ЃЉ![]() _____________ЃЌ
_____________ЃЌ![]() ____________ЃЛ
____________ЃЛ
ЃЈ2ЃЉЧѓЯњЪлРЖнЎЕкМИЬьЪБЃЌЕБЬьЕФРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉдкЯњЪлРЖнЎЕФ30ЬьжаЃЌЕБЬьРћШѓВЛЕЭгк870дЊЕФЙВгаЖрЩйЬьЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
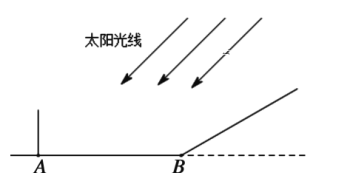
ЁОЬтФПЁПаЁЗМЩэИп1.6УзЃЌДЫЪБЬЋбєЙтЯпгыЕиУцЕФМаНЧЮЊ45ЁуЃЎ
ЃЈ1ЃЉШєаЁЗМе§еОдкЫЎЦНЕиУцAДІЩЯЪБЃЌФЧУДЫ§ЕФгАГЄЮЊЖрЩйУзЃП
ЃЈ2ЃЉШєаЁЗМРДЕНвЛИіЦТЖШi=![]() ЕФЦТУцЕзЖЫBДІЃЌЕБЫ§дкЦТУцЩЯжСЩйЧАНјЖрЩйУзЪБЃЌаЁЗМЕФгАзгЧЁКУЖМТфдкЦТУцЩЯЃП
ЕФЦТУцЕзЖЫBДІЃЌЕБЫ§дкЦТУцЩЯжСЩйЧАНјЖрЩйУзЪБЃЌаЁЗМЕФгАзгЧЁКУЖМТфдкЦТУцЩЯЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com