
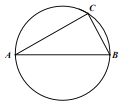
【题目】如图,已知△ABC及其外接圆,∠C=90°,AC=10.
(1)若该圆的半径为5![]() ,求∠A的度数;
,求∠A的度数;
(2)点M在AB边上(AM>BM),连接CM并延长交该圆于点D,连接DB,过点C作CE垂直DB的延长线于E.若BE=3,CE=4,试判断AB与CD是否互相垂直,并说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=![]() (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售甲、乙两种圆规,当销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元.
(1)问该文具店销售甲、乙两种圆规,每只的利润分别是多少元?
(2)在(1)中,文具店共销售甲、乙两种圆规50只,其中甲种圆规为a只,求文具店所获得利润P与a的函数关系式,并求当a≥30时P的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,关于此函数的图象及性质,下列结论中不一定成立的是( )
,关于此函数的图象及性质,下列结论中不一定成立的是( )
A.该图象的顶点坐标为![]() B.该图象与
B.该图象与![]() 轴的交点为
轴的交点为![]()
C.若该图象经过点![]() ,则一定经过点
,则一定经过点![]() D.当
D.当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:两个相似等腰三角形,如果它们的底角有一个公共的顶点,那么把这两个三角形称为“关联等腰三角形”.如图,在![]() 与
与![]() 中,
中,![]() ,且
,且![]() 所以称
所以称![]() 与
与![]() 为“关联等腰三角形”,设它们的顶角为
为“关联等腰三角形”,设它们的顶角为![]() ,连接
,连接![]() ,则称
,则称![]() 会为“关联比".
会为“关联比".
下面是小颖探究“关联比”与α之间的关系的思维过程,请阅读后,解答下列问题:
[特例感知]
![]() 当
当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,
时,
①在图1中,若点![]() 落在
落在![]() 上,则“关联比”
上,则“关联比”![]() =
=
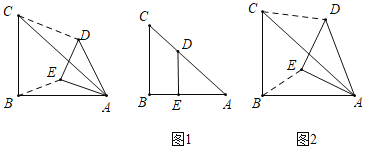
②在图2中,探究![]() 与
与![]() 的关系,并求出“关联比”
的关系,并求出“关联比”![]() 的值.
的值.

[类比探究]
![]() 如图3,
如图3,
①当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,“关联比”
时,“关联比”![]() =
=
②猜想:当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,“关联比”
时,“关联比”![]() = (直接写出结果,用含
= (直接写出结果,用含![]() 的式子表示)
的式子表示)
[迁移运用]
![]() 如图4,
如图4, ![]() 与
与![]() 为“关联等腰三角形”.若
为“关联等腰三角形”.若![]() 点
点![]() 为
为![]() 边上一点,且
边上一点,且![]() ,点
,点![]() 为
为![]() 上一动点,求点
上一动点,求点![]() 自点
自点![]() 运动至点
运动至点![]() 时,点
时,点![]() 所经过的路径长.
所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区组织了以“奔向幸福,‘毽’步如飞”为主题的踢毽子比赛活动,初赛结束后有甲、乙两个代表队进入决赛,已知每队有5名队员,按团体总数排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是两队各队员的比赛成绩.
1 号 | 2 号 | 3 号 | 4 号 | 5 号 | 总数 | |
甲队 | 103 | 102 | 98 | 100 | 97 | 500 |
乙队 | 97 | 99 | 100 | 96 | 108 | 500 |
经统计发现两队5名队员踢毽子的总个数相等,按照比赛规则,两队获得并列第一.学习统计知识后,我们可以通过考查数据中的其它信息作为参考,进行综合评定:
(1)甲、乙两队的优秀率分别为 ;
(2)甲队比赛数据的中位数为 个;乙队比赛数据的中位数为 个;
(3)分别计算甲、乙两队比赛数据的方差;
(4)根据以上信息,你认为综合评定哪一个队的成绩好?简述理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作⊙
的长为半径作⊙![]() ,过点
,过点![]() 作
作![]() 的垂线交⊙
的垂线交⊙![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,以
,以![]() ,
,![]() 为边作
为边作![]() .
.
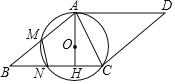
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求四边形
,求四边形![]() 与⊙
与⊙![]() 重叠部分的面积;
重叠部分的面积;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 和
和![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠B=60°,AB=2,M为边AB的中点,N为边BC上一动点(不与点B重合),将△BMN沿直线MN折叠,使点B落在点E处,连接DE、CE,当△CDE为等腰三角形时,BN的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,![]() ,AC、BD交于点O,点P、Q分别是AB、BD上的动点,点P的运动路径是
,AC、BD交于点O,点P、Q分别是AB、BD上的动点,点P的运动路径是![]() ,点Q的运动路径是BD,两点的运动速度相同并且同时结束.若点P的行程为x,
,点Q的运动路径是BD,两点的运动速度相同并且同时结束.若点P的行程为x,![]() 的面积为y,则y关于x的函数图象大致为( )
的面积为y,则y关于x的函数图象大致为( )
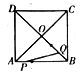
A.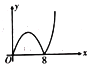 B.
B.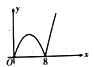 C.
C. D.
D.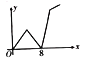
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com