
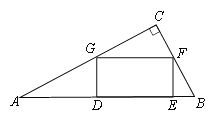
【题目】如图,在Rt△ABC中,∠C=90°,矩形DEFG的顶点G、F分别在边AC、BC上,D、E在边AB上.
(1)求证:△ADG∽△FEB;
(2)若AD=2GD,则△ADG面积与△BEF面积的比为 .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
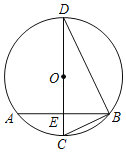
【题目】如图,CD是⊙O的直径,AB是⊙O的弦,CD⊥AB,垂足为E,连接BC、BD.点F为线段CB上一点,连接DF,若CE=2,AB=8,BF=![]() ,则tan∠CDF=__.
,则tan∠CDF=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个二次函数图象上部分点的横坐标x与纵坐标y的对应值如下表所示:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
(1)求这个二次函数的表达式;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)当4<x<1时,直接写出y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级(1)班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,恰好选到男生是 事件(填随机或必然),选到男生的概率是 .
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图的方法,求刚好是一男生和一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
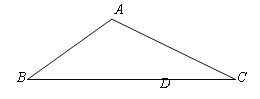
【题目】如图,在△ABC中,AB=3,AC=4,BC=6,D是BC上一点,CD=2,过点D的直线l将△ABC分成两部分,使其所分成的三角形与△ABC相似,若直线l与△ABC另一边的交点为点P,则DP=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知近视眼镜的度数y(度)与镜片焦距x(米)之间成如图所示的反比例函数关系,则眼镜度数y与镜片焦距x之间的函数解析式为( )

A. y=200x B. y=![]() C. y=100x D. y=
C. y=100x D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() ,
,![]() .
.
(1)求该抛物线的函数表达式及对称轴;
(2)设点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 是抛物线对称轴上一动点,记抛物线在
是抛物线对称轴上一动点,记抛物线在![]() ,
,![]() 之间的部分为图象
之间的部分为图象![]() (包含
(包含![]() ,
,![]() 两点),如果直线
两点),如果直线![]() 与图象
与图象![]() 有一个公共点,结合函数的图象,直接写出点
有一个公共点,结合函数的图象,直接写出点![]() 纵坐标
纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)P是抛物线上的第一象限内的动点,过点P作PMx轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.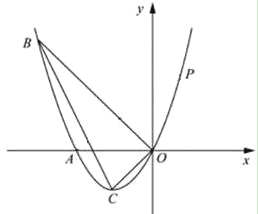
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com