练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
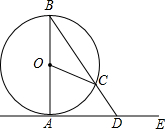
    11．如图，AB是⊙O直径，点C在⊙O上，AE是⊙O的切线，A为切点，连接BC并延长交AE于点D．若∠AOC=80°，则∠ADB的度数为（　　）
    A．40°B．50°C．60°D．20°

    分析 由AB是⊙O直径，AE是⊙O的切线，推出AD⊥AB，∠DAC=∠B=$\frac{1}{2}$∠AOC=40°，推出∠AOD=50°．

    解答 解：∵AB是⊙O直径，AE是⊙O的切线，
    ∴∠BAD=90°，
    ∵∠B=$\frac{1}{2}$∠AOC=40°，
    ∴∠ADB=90°-∠B=50°，
    故选B．

    点评 本题主要考查圆周角定理、切线的性质，解题的关键在于连接AC，构建直角三角形，求∠B的度数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

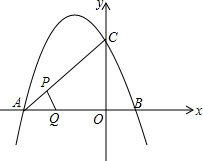    1．如图，二次函数y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4的图象与x轴交于A，B两点（点B在点A的右侧），与y轴交于点C，若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿线段AC，AB运动，其中一点到达端点时，另一点也随之停止运动．
    （1）求点A，B，C的坐标；
    （2）当点Q运动到B点时，点P停止运动，这时x轴上是否存在点D，使得以A，P，D为顶点的三角形为等腰三角形？若存在，请求出D点坐标；若不存在，请说明理由；
    （3）当P，Q运动到t秒时，△APQ沿PQ翻折，点A恰好落在抛物线上F点处，请断定此四边形APFQ的形状，并求出此时点F的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

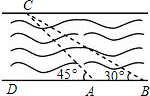    2．如图所示，我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度．小宇同学在A处观测对岸C点，测得∠CAD=45°，小英同学在距A处50米远的B处测得∠CBD=30°，请你根据这些数据算出河宽．（精确到0.01米，参考数据$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于（　　）
    A．10B．7C．5D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图，AB∥CD，直线l分别与AB，CD相交，若∠1=50°，则∠2的度数为50°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，△ABC中，CD是边AB上的高，且$\frac{AD}{CD}$=$\frac{CD}{BD}$．
    （1）求证：△ACD∽△CBD；
    （2）求∠ACB的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．根据某网站调查，2014年网民们最关注的热点话题分别有：消费、教育、环保、反腐及其他共五类．根据调查的部分相关数据，绘制的统计图表如下：

    根据所给信息解答下列问题：
    （1）请补全条形统计图并在图中标明相应数据；
    （2）若菏泽市约有880万人口，请你估计最关注环保问题的人数约为多少万人？
    （3）在这次调查中，某单位共有甲、乙、丙、丁四人最关注教育问题，现准备从这四人中随机抽取两人进行座谈，试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．解不等式组$\left\{\begin{array}{l}{-2x＜6①}\\{3（x+1）≤2x+5②}\end{array}\right.$，并将解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．一个不透明的袋子中只装有3个黑球，2个白球，这些球的形状、大小、质地等完全相同，即除颜色外无其他差别．在看不到球的条件下，随机从袋中摸出1个球，则摸出白球的概率是$\frac{2}{5}$．

    查看答案和解析>>

    同步练习册答案