
【题目】为了倡导低碳交通,方便市民出行,某市推出了公共自行车系统,收费以小时为单位,每次使用不超过1小时的免费,超过1小时后,不足1小时的部分按1小时收费,小聪同学通过调查得知,自行车使用时间为3小时,收费2元;使用时间为4小时,收费3元.她发现当使用时间超过1小时后用车费与使用时间之间存在一次函数的关系.
(1)设使用自行车的费用为y元,使用时间为x小时(x为大于1的整数),求y与x的函数解析式;
(2)若小聪此次使用公共自行车6小时,则她应付多少元费用?
(3)若小聪此次使用公共自行车付费7元,请说明她所使用的时间的范围.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. a不是负数,则a>0 B. b是不大于0的数,则b<0
C. m不小于﹣1,则m>﹣1 D. a,b是负数,则a+ b<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)![]() ﹣(+3.7)+(+
﹣(+3.7)+(+ ![]() )﹣(﹣1.7)
)﹣(﹣1.7)
(2)( ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣24)
)×(﹣24)
(3)﹣32×(﹣2)+42÷(﹣2)3﹣|﹣22|
(4)﹣27÷2 ![]() ×
× ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为a cm的正方形内,截去两个以正方形的边长a cm为直径的半圆,(结果保留π) 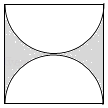
(1)图中阴影部分的周长为cm.
(2)图中阴影部分的面积为cm2 .
(3)当a=4时,求出阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,点M(1,2)关于x轴对称的点的坐标为( )
A. (﹣1,2) B. (2,﹣1) C. (﹣1,﹣2) D. (1,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据给出的数轴及已知条件,解答下面的问题: ![]()
(1)已知点A,B,C表示的数分别为1,﹣ ![]() ,﹣3观察数轴,与点A的距离为3的点表示的数是 , B,C两点之间的距离为;
,﹣3观察数轴,与点A的距离为3的点表示的数是 , B,C两点之间的距离为;
(2)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是;若此数轴上M,N两点之间的距离为2015(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则M,N两点表示的数分别是:M , N;
(3)若数轴上P,Q两点间的距离为m(P在Q左侧),表示数n的点到P,Q两点的距离相等,则将数轴折叠,使得P点与Q点重合时,P,Q两点表示的数分别为:P , Q(用含m,n的式子表示这两个数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线的方程C1: ![]() (m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(1)若抛物线C1过点M(2, 2),求实数m的值;
(2)在(1)的条件下,求△BCE的面积;
(3)在(1)的条件下,在抛物线的对称轴上找一点H,使得BH+EH最小,求出点H的坐标;
(4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com